Table d’azimut et navigation celeste: un exemple pratique d’utilisation
L’azimut Zv: compté à partir du point cardinal nord, de 0° à 360° (dans le sens des aiguilles d’un montre)
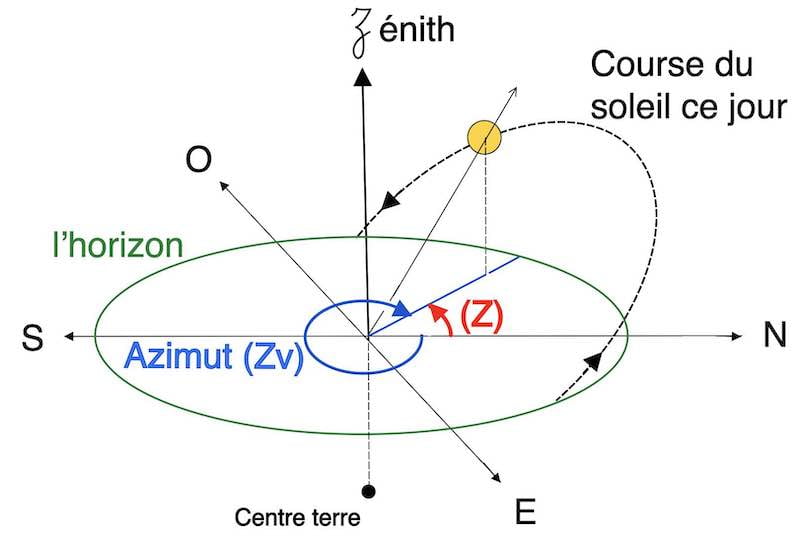
Nos formules ou tables fournissent des résultats (Z) dans la plage de 0° à 180°.
Table d’azimut et navigation celeste: comment transformer Z en Zv?
1) Pour les formules:

Cette formule génère une réponse azimut (Z) entre 0° et 180°. Il est à nous de la transformer en azimut vrai (Zv) dans une notation entre 0° et 360°.
Si l’on observe le soleil à l’est, alors 𝑍𝑣 = 𝑍.
Si on l’observe à l’ouest, alors 𝑍𝑣 = 360°− 𝑍
L’image ci-dessus nous montre le soleil à l’ouest. Alors 𝑍𝑣 =3 60°−𝑍
2)Pour les tables d’azimut:
Veuillez vous référer à l’exemple plus bas sur cette page
L’horizon locale:

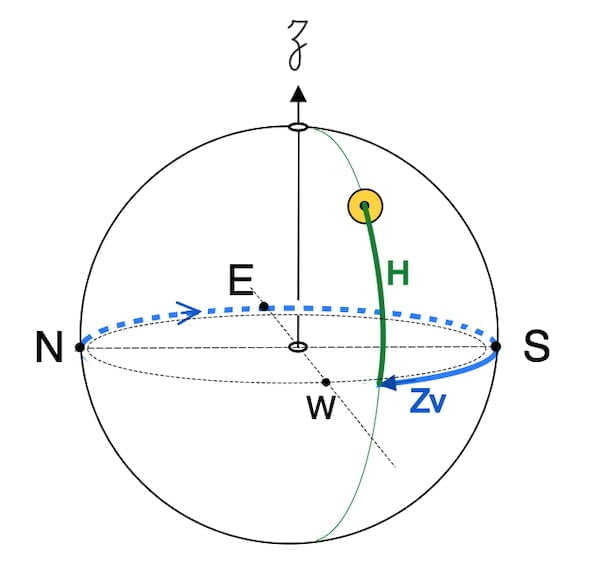


Table d’azimut et navigation celeste: explication et un exemple pratique des tables d’azimut
Technique utilisée: l’azimut par l’heure
Après avoir trouvé le hauteur calculée, il faut trouver l’azimut Zv à un demi degré près.
Les tables que je présente sont un peu plus volumineuses que les tables d’azimut classiques, car la lecture se fait toujours de haut en bas et non pas dans les deux sens, technique utilisée pour réduire la quantité de feuilles mais qui peut parfois être pénible à utiliser.
Je ne vois pas d’autre méthode pour expliquer les tables d’azimut que par un exemple.
Dans ce cours, vous trouverez un exemple sur cette page, quatre exercices avec leurs réponses, et l’exercice de La Rochelle, ce qui fait un total de cinq exercices avec explication et solution complètes.
Les feuilles des tables d’azimut nécessaires pour ces exercices sont fournies, mais la totalité de ces tables ne peut être téléchargée qu’après l’achat dans la boutique.
L’utilisation des tables peut être un peu laborieuse au départ, mais après avoir fait tous ces exercices et peut-être une deuxième fois, vous verrez que vous allez apprécier les explications qui se trouvent toujours dans la marge de chaque feuille de ces tables et il se peut que vous maîtrisiez mieux les tables, que le calcul Zv avec la calculatrice scientifique.
Notre feuille de calcul

Nos tables d’azimuth: Part 1 et Part 2
Part 1 :
Entrée: P, D et L
Sortie: zc et acute ou obtuse pour Z




Part 2 :
Cette table contient deux sous_tables
Z = 0 à 90 degrés (aigu → acute)
Z = 90 à 180 degrés (obtus → obtuse).


Entrée: L et zc (sous table acute ou obtuse)
Sortie:
1) Z
2) Zv après consideration P = NE/NO/SE/SO


Ici un exemple pratique:
Table d’azimut et navigation celeste: part 1
Partie 1 :
Saisie L, D et P:
Résultat: (1) zc et (2) aigu ou obtus.
(L)atitude estimée = 12° N
(D)éclinaison soleil = 17° S
L’angle au (P)ôle = 10° NO
(soleil à l’Ouest, l’hémisphère Nord)
(Ne pas confondre avec longitude Ouest)
Table d’azimut part 1

lc = 1,21; dc = 1,76
Table d’azimut et navigation celeste
aigu (acute)
obtus (obtuse)

La règle des signes n’est plus utilisée, mais plutôt « même nom » ou « nom différent » comme indiqué dans les tableaux. (same name ou not same name)

Dans notre exemple:
L et D NOT SAME name
(L = Nord et D = Sud)
P < 90°

Conclusion:
zc = lc + dc (1,21 + 1,76 = 2,97)
Z = obtuse (entre 90° et 180°)
On passe à part 2
Table d’azimut et navigation celeste: part 2
Partie 2:
Saisie zc et aigu ou obtus (obtenu en part 1)
Résultat Zv.
Attention, Attention, dans part 2 des tables d’azimut, il y a deux volets différents !
les pages aigu (acute) (Z = 0° jusqu’à 90°)
les pages obtus (obtuse) (Z = 90° jusqu’à 180°).
Avec la latitude L (12° N) et zc (2,97) on obtient Z. (Z est obtus dans notre exemple)

Dans les deux cas (acute et obtuse), le trait horizontal de la latitude (12°N) affiche quelque part la valeur zc = 2,97.
Attention c’est la ou c’est facile de se tromper!
(aigu) acute

(obtus) obtuse

Z est donc 161°
Mais on doit trouver Zv ( notation modern de 0° – 360°)
Dans la marge à droite de chaque page dans la partie 2 on trouve les deux tableaux ci-dessous
Azimut table: Part 2

Avec latitude Nord et P = NO
Z = 161°