Exemple de Calcul de la hauteur du Soleil et tables de logarithmes
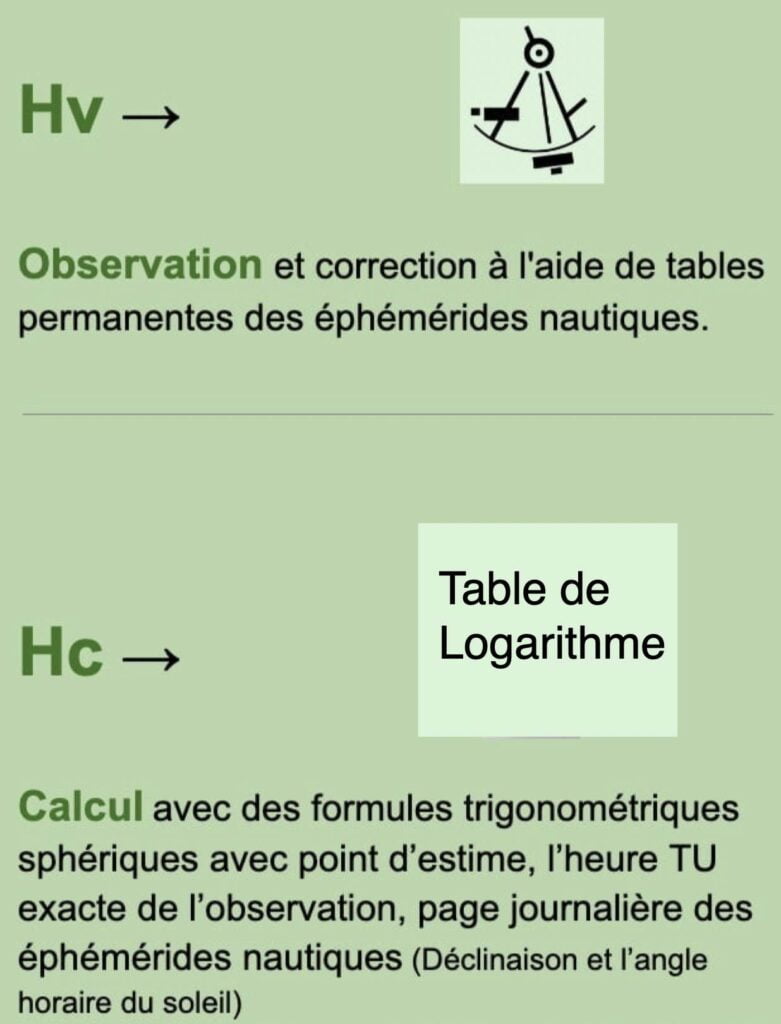

Exemple de calcul de la hauteur du soleil et logarithmes


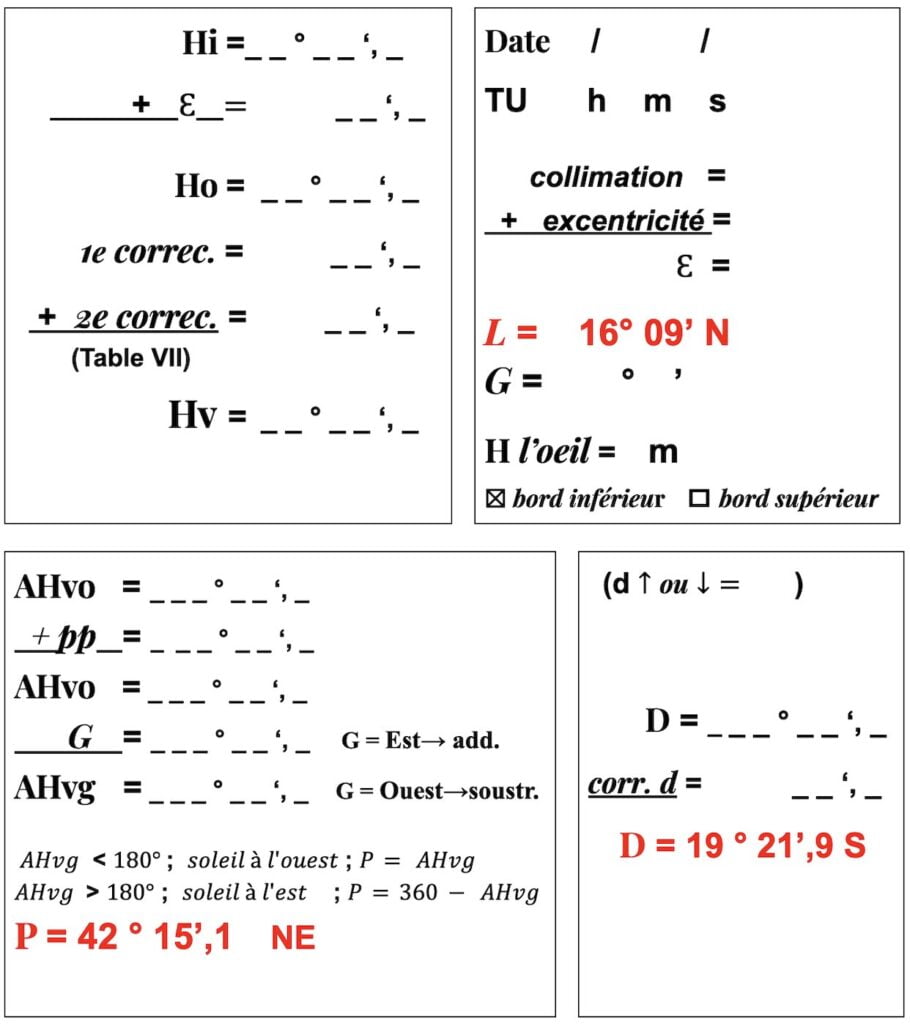

Les entrées obtenues dans la première partie du feuille de calcul nécessaires pour trouver la hauteur calculée (Hc) sont :
L = 16° 09′ N
D = 19°21′,9 S
P = 42°15′,1
Calcul Hc
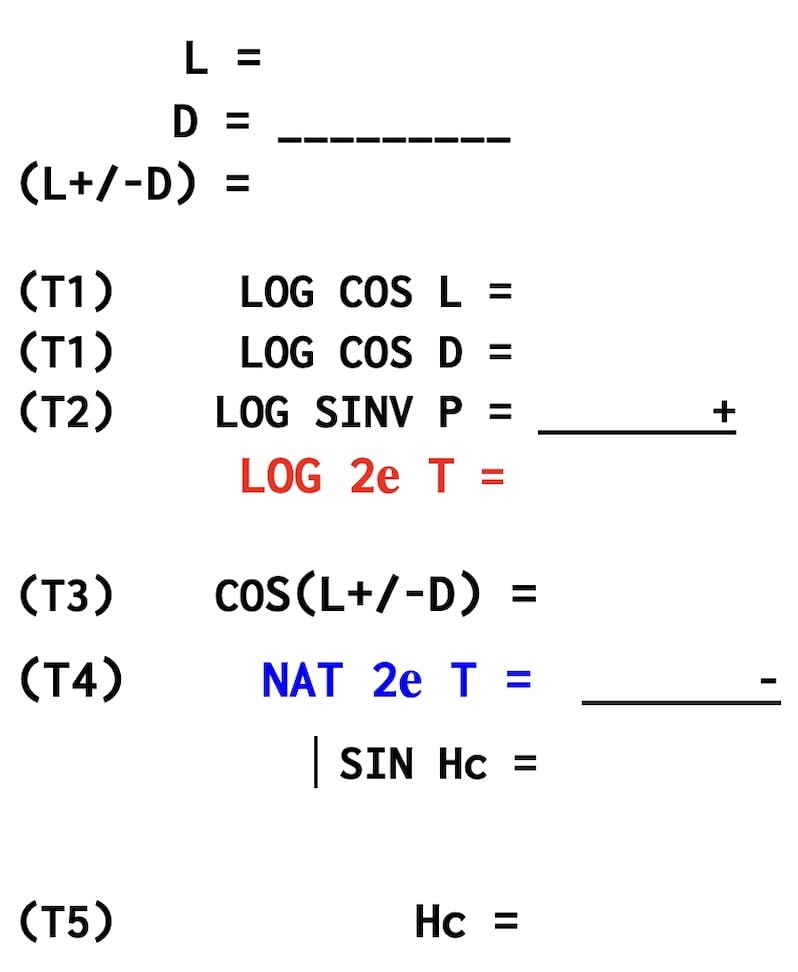
Etape 1


L = 16° 09′ N
D = 19°21′,9 S
__________________
(L +D) = 35° 30′,9 (not same name)
4 exemples same name/not same name
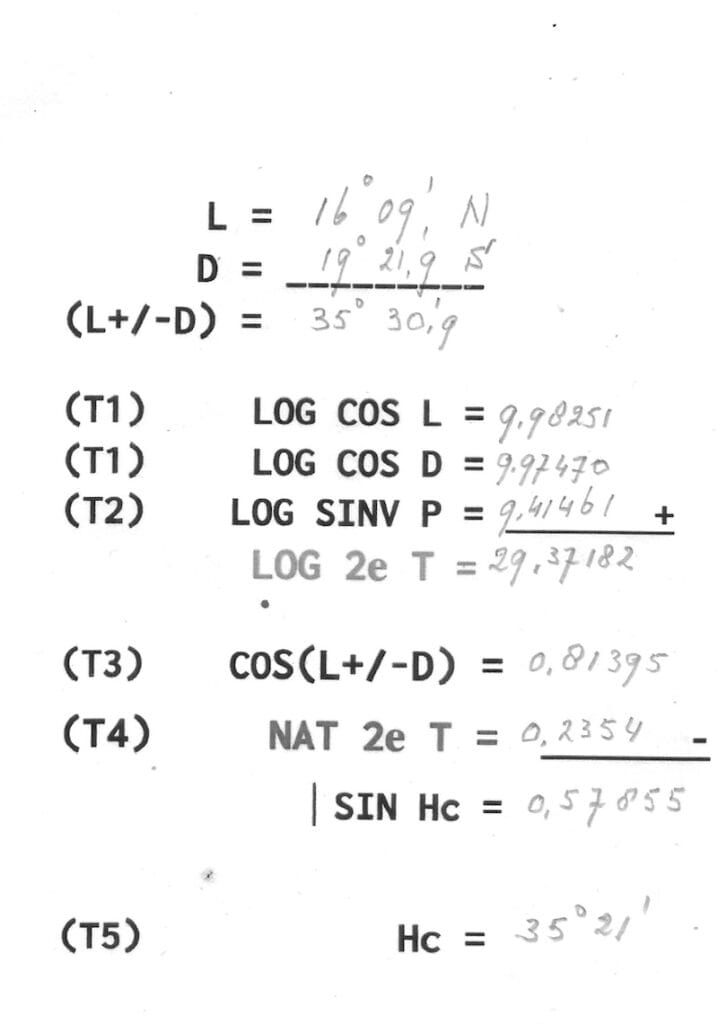
Etape 2

1 (T 1 ) LOG COS L = 9,98251
2 (T 1 ) LOG COS D = 9,97470
3 (T 2 ) LOG SINUS VERSE P = 9,41461
__________________________________+
LOG 2e Terme = 29,37182
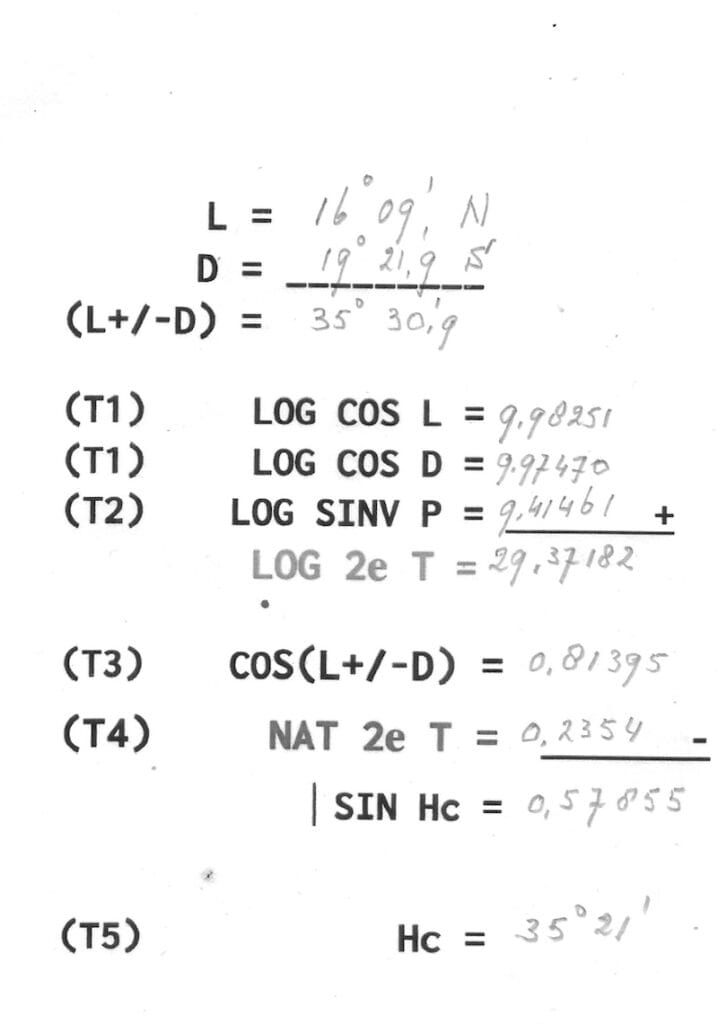
Etape 3
Comment transformer un logarithme en sa valeur naturelle ?
Log 2e T → Nat 2e T
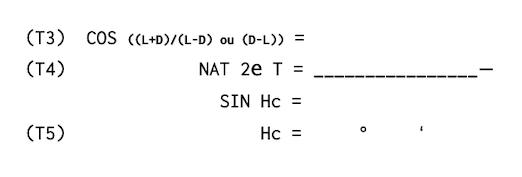
(T 3) COS (L / D) = 0,81395. Etape 1
(T4 ) Nat 2e T = 0,2354.
_______________________________-
SIN Hc = 0,57855
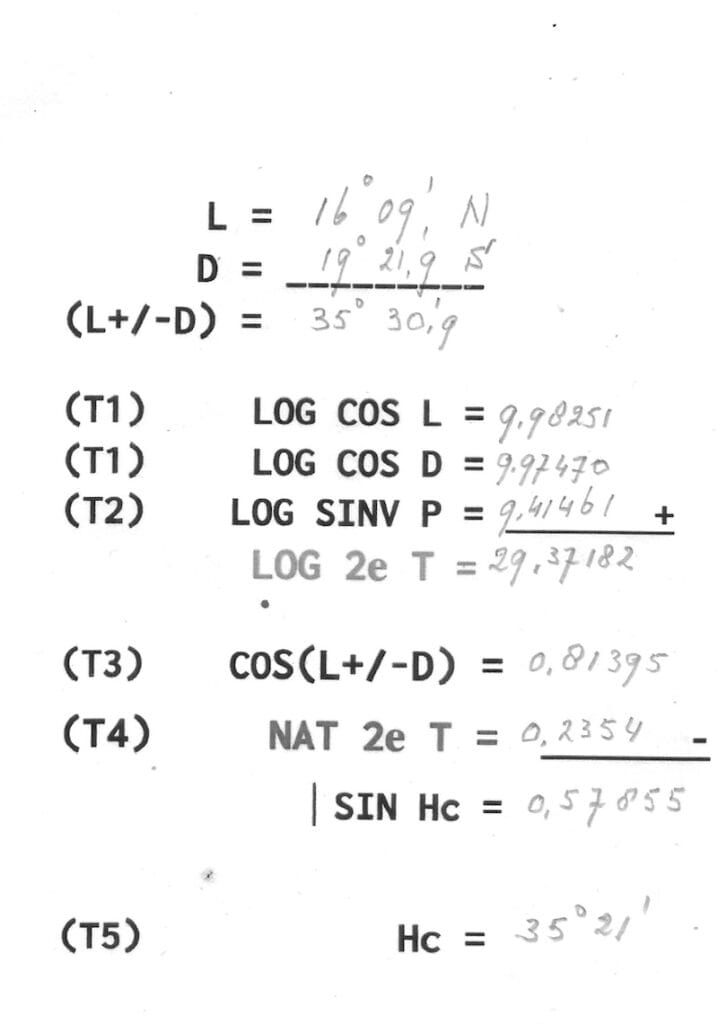
Etape 4
(T 5) Hc = 35°21′
Une fois cet exemple compris, vous pouvez poursuivre vers la page qui contient deux exercices construits sur le même modèle.
conclusion
En conclusion, les tables de logarithmes ont joué un rôle crucial dans l’histoire maritime en simplifiant les calculs mathématiques nécessaires à la navigation.
Au cours des siècles passés, avant l’avènement des calculatrices et des ordinateurs, les marins devaient se fier à des instruments et des techniques de navigation traditionnelles pour traverser les océans.
Les tables de logarithmes, inventées par le mathématicien écossais John Napier au début du XVIIe siècle, étaient une aide précieuse pour les marins.
Ces tables répertoriaient les logarithmes (les exposants d’une série de nombres) pour faciliter les multiplications et les divisions. En utilisant les tables de logarithmes, les marins pouvaient effectuer des calculs complexes.
Dans ce cours, je ne me concentre pas sur la compréhension du fonctionnement de l’univers des logarithmes, mais plutôt sur l’utilisation pratique des tables de logarithmes.
Plus précisément, je mets l’accent sur l’utilisation de la table des logarithmes pour les nombres entiers, dont la lecture n’est pas intuitive. Cependant, une fois maîtrisée, cette table devient presque aussi simple à employer que le bouton “log” d’une calculatrice.