
Explication des tables de logarithmes (théorie)
Réponse exercice table Hc exemple
Les tables ci-dessous ne sont pas très lisibles puisqu’ils ont été transformé en fichiers jpeg.
Table 1

log cosinus 16°09′ (latitude)
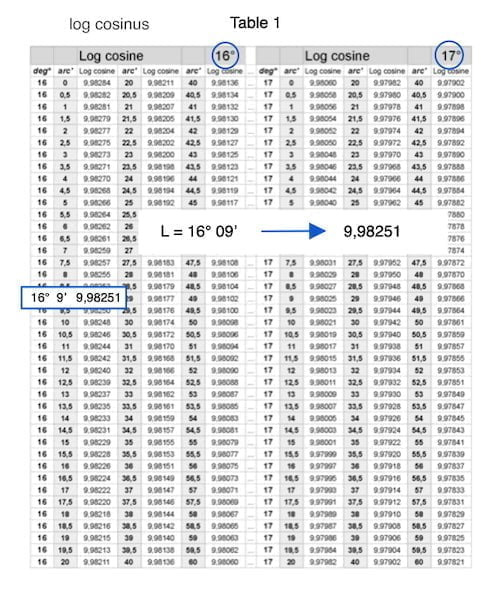
log cosinus 16° 09’ sur notre calculatrice scientifique nous donne -0,017485.
Il est néanmoins beaucoup plus commode de mettre ces sortes de logarithmes sous forme de quantités positives.
Des tables américaines se présentent alors sous la forme suivante:
10 + (-0,017485) = 9,98251
En France dans les tables de logarithmes et de navigation de Georges Friocourt, au lieu de rajouter 10, on rajoute 1
Ici on utilise les tables types américaines
Log cosinus 19° 21′,9 (Déclinaison)
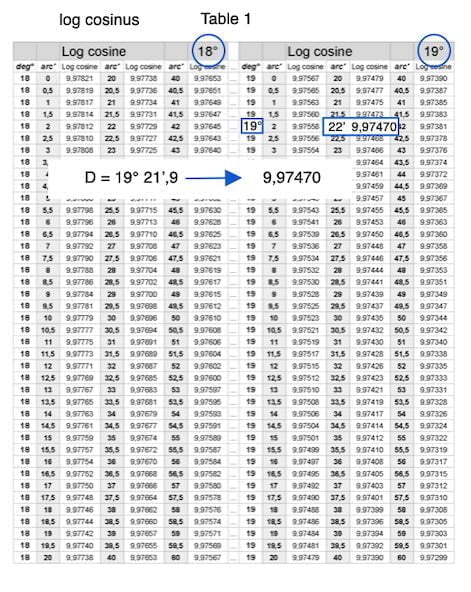
Table 2

Log sinus verse 42° 15′,1 l’angle au pôle

Table 3

cosinus 35° 30′,9
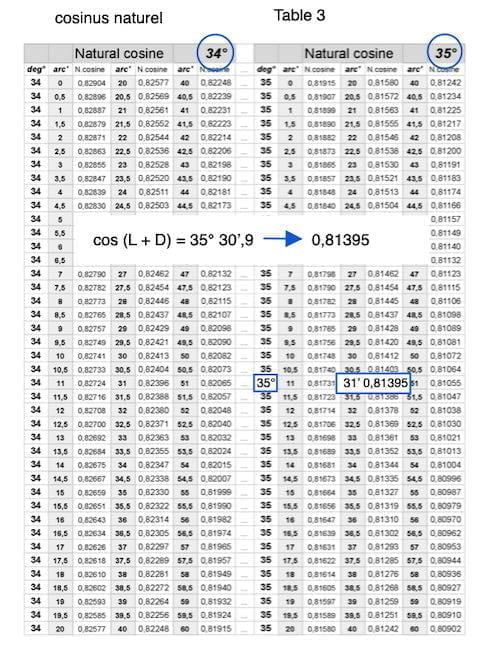
Réponse exercice table Hc exemple
table 4
Log 2e T vers Nat 2 T
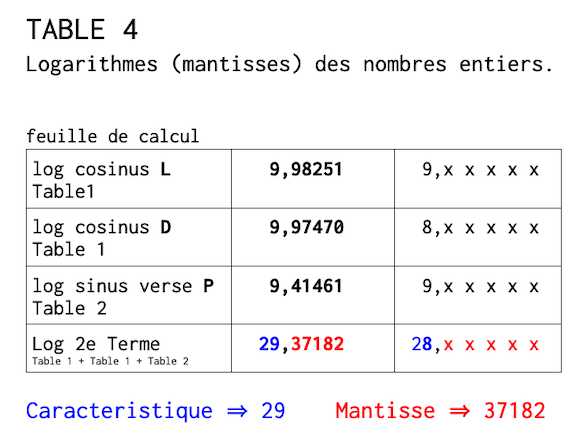
Avec la Mantisse, nous chercherons le nombre entier.
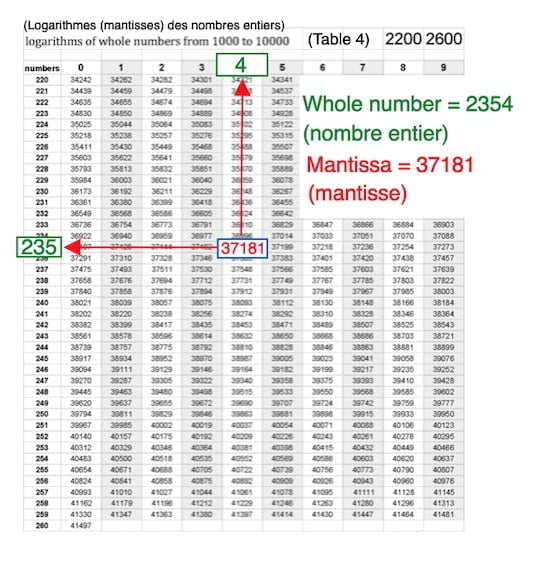
Après avoir trouvé le nombre entier, nous devons mettre la virgule !

Naturel 2e T. = 0,2354
Table 5
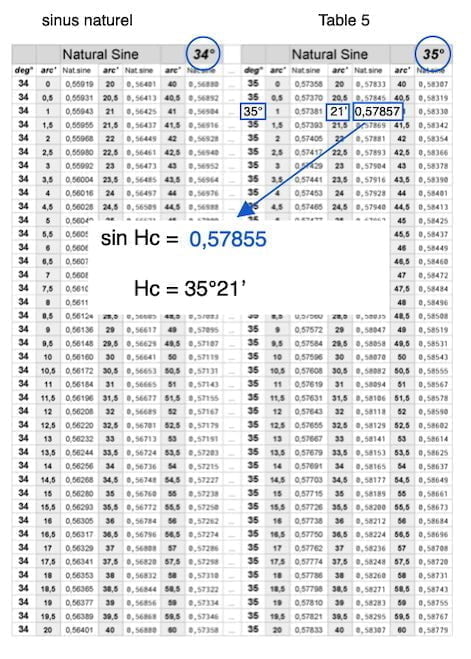
Avec une calculatrice : arcsin (0.57855) = 35° 21′
Remarque final:
Le tableau 4 peut ne pas être intuitif au départ, mais il devient facile à utiliser une fois que l’on connaît les règles pour l’utiliser.
Il peut arriver que les données d’entrée dans le tableau ne correspondent pas exactement aux valeurs présentes dans le tableau. Dans ce cas, il est nécessaire d’utiliser des techniques d’interpolation linéaire entre deux valeurs du tableau. On peut estimer ces interpolations et on tolère de petites erreurs.
En utilisant les tableaux comme outil, il n’est pas nécessaire d’avoir de vastes connaissances dans le monde parfois complexe des logarithmes.
On peut utiliser les tableaux pour le soleil, la lune, les planètes et les étoiles (latitude maximale et déclinaison de 68° Nord et Sud), et les tableaux ne dépendent pas du temps.