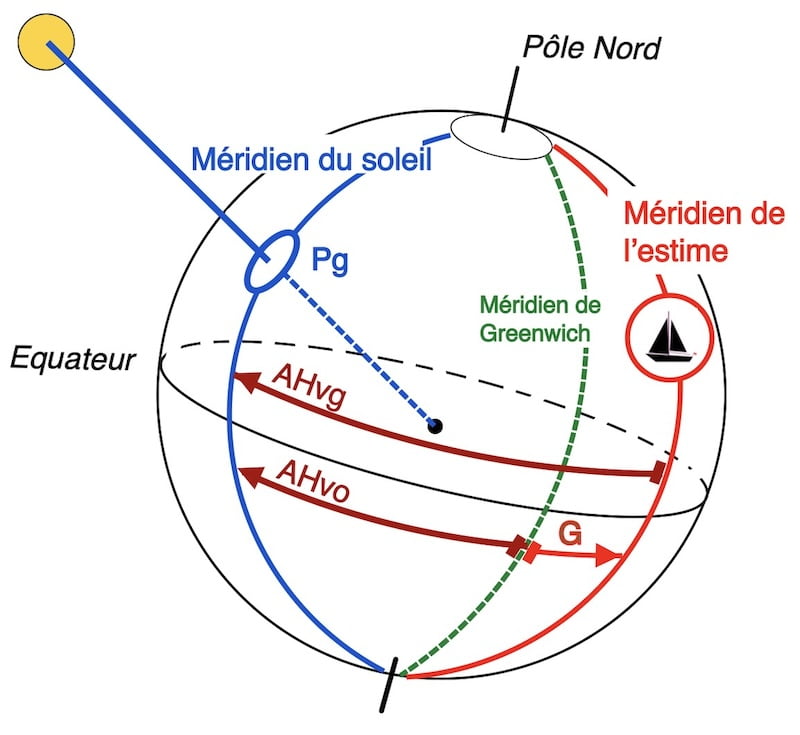
Sur cette page l’angle horaire locale et l’angle au pôle, nous établissons une corrélation entre la longitude estimée de l’observateur et l’Angle Horaire au méridien de Greenwich (AHvo) du Soleil, désigné comme l’Angle Horaire Local (AHvg).

D’abord, pour des raisons mathématiques, nous effectuons une transformation de l’angle AHvg (0° – 360°) vers l’angle au pôle P (0° – 180°), nécessitant une condition spécifique expliquée en détail sur cette page.


équivalent en anglais
attention: AHvo → en anglais (GHA) Greenwich hour angle
AHvg → en anglais (LHA ) Local hour angle



Par ailleurs, avant de lire cette page:
vous devriez revoir la théorie de la déclinaison D
et de l’angle horaire du Soleil à Greenwich (AHvo).

Définition de l’angle horaire local (AHvg)
Alors, on établit l’angle entre le méridien de sa position de l’estime (G) et le méridien du soleil
AHvg = AHvo – G
convention des signes en France:
Nord +
Sud –
Est –
Ouest +
En revanche, ne pas confondre avec la déclinaison magnétique qui est négatif Ouest et positif Est

AHvo…….= _ _° _ _’, _
**G………..= _ _ ° _ _ ‘, _
_____________________+/-
AHvg……..= _ _ ° _ _ ‘, _
Finalement, en appliquant la convention des signes on peut conclure qu’il faut additionner la longitude Est et soustraire la longitude Ouest pour la relation AHvg = AHvo – G
**G ajouter si G est Est / soustraction si G est Ouest

AHvo/AHvg
AHvo…….= _ _ ° _ _ ‘, _
pp………….= _ _° _ _’, _
____________________+
AHvo…….= _ _° _ _’, _
**G………..= _ _ ° _ _ ‘, _
_____________________+/-
AHvg……..= _ _ ° _ _ ‘, _
P……………..= _ _ ° _ _ ‘, _
En conclusion, **G addition si G est Est / soustraction si G est Ouest

L’extrait provient de l’ouvrage intitulé ‘Types de calculs nautiques’,

Par ailleurs, l’ouvrage qui porte le numéro 109, et qui était utilisé à l’école anciennement appelée l’École Nationale de la Marine Marchande du Havre, pour les élèves de première année
En outre, le symbole ‘v‘ est utilisé pour le soleil

Conversion vers l’angle au pôle (P)
L’angle au pôle (P)
D’abord, au lieu d’utiliser l’angle horaire locale AHvg 0° à 360° comme angle on peut utiliser l’angle au pôle qui se chiffre entre 0° à 180° à condition;
AHvg < 180°
⟹ Soleil à l’Ouest
⟹ P = AHvg
Exemple: AHvg = 110°
⟹ P = 110°
AHvg > 180°
⟹ Soleil à l’Est
⟹ P = 360° ㆒ AHvg
Exemple: AHvg = 300°
⟹ P = 360° – 300° = 60°

l’angle horaire locale et l’angle au pôle: Triangle de position
En effet, l’angle au pôle (P) constitue l’une des 3 clés de la résolution trigonométrique du triangle de position.
Toutefois, la résolution du triangle sphérique avec ces formules fondamentales (entre autre la formule des cosinus) et le passage des coordonnées horaires vers les coordonnées horizontales sont complex.

La compréhension de ce triangle de position ainsi que les formules générées à partir de ce triangle ne sont pas nécessaires pour le déroulement sur notre grille de calcul.
En outre, ces deux formules sont intégrées sur cette grille de calcul.
la résolution du triangle sphérique
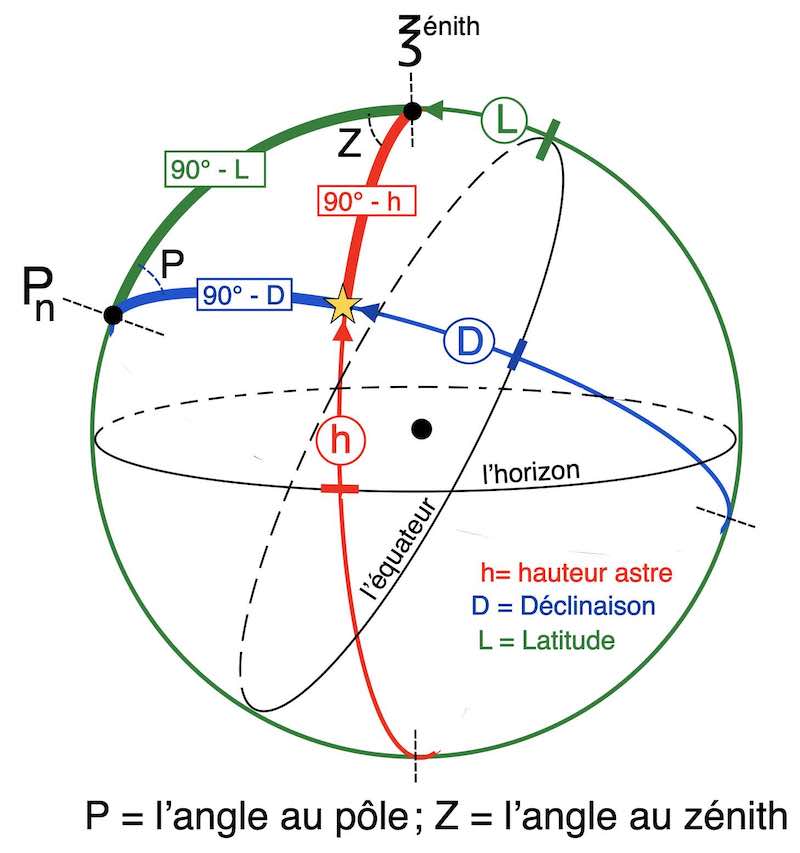
Ce site ladroitedehauteur.com n’a pas pour objectif d’expliquer le triangle de position en soi; il se concentre plutôt sur l’application des formules qui en sont dérivées.



Conclusion et application pratique
En somme, pour calculer une droite de hauteur en haut mer ou dans une salle d’examen, la compréhension de la résolution trigonométrique du triangle sphérique semble être d’importance relativement mineure.
Puis, les formules n’ont pas besoin d’être mémorisées puisqu’elles sont déjà incluses dans notre feuille de calcul.

En effet, ce qui importe, c’est le juste remplissage de la grille classique St Marcq Hilaire ( notre feuille de calcul ) avec le respect des signes de convention
Finalement, cela demande un entraînement…