De l’altitude mesurée au sextant (Hi) à l’altitude observée (Ho): Exemple calcul Ho

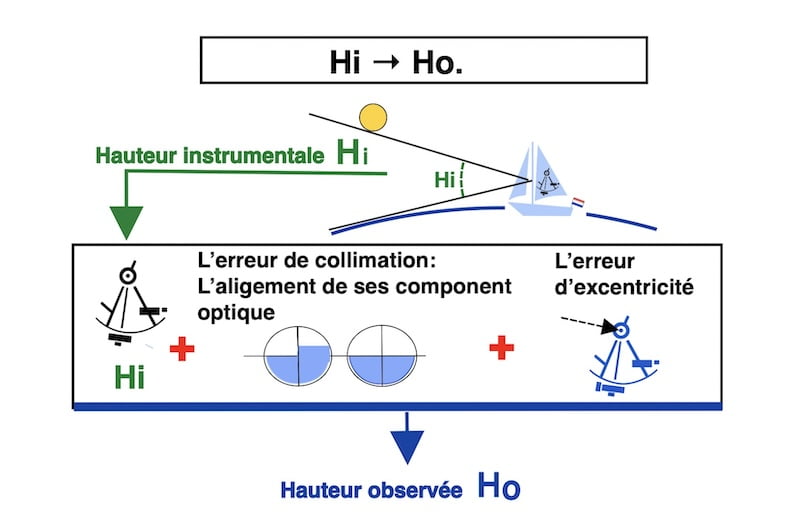
Après avoir mesuré la hauteur du soleil avec un sextant, il est essentiel d’appliquer les corrections spécifiques liées à l’instrument, telles que la correction de la collimation et de l’excentricité, pour obtenir la hauteur observée.



Corrections du sextant en un coup d’œil
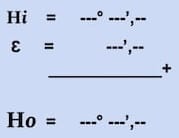
1) Hi →Ho. – THEORIE.
2) Hi →Ho. – CALCUL (sur cette page!)
3) Ho →Hv. – THEORIE
4) Ho →Hv. – CALCUL
Trois exercices complets avec réponses : de Hi à Hv (page 4)

Un rapide aperçu des quatre pages de correction du sextant et de leurs points clés (de la page 1 à la page 4, dans cet ordre).

Exemple pratique du calcul de Hi vers Ho



Hi = Hauteur instrumentale = 74°06′

erreur de collimation = +0°07′ = +7′

Hi = 74°06′ à peu près 75° donc l’erreur d’excentricité est +0°01′ = +1′
ε = collimation + erreur d’excentricité
= (+ 7′) + (+ 1′) = + 8′

Hi……………… = 74° 06′, 0
+ Ɛ …………….. = 00° 08’,0
_______________________ +
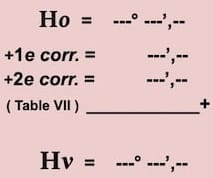
Ho……………….= 74 14’, 0
+ 1e correc…… = _ _° _ _’, _
+ 2e correc….. = _ _° _ _’, _
( Table VII )
_______________________ +
Hv………………..= _ _° _ _’, _

Observations calcul Hi vers Ho
La lecture précise d’un sextant (Hi), correctement ajusté, offre une précision angulaire de environ 0,2 minutes d’arc. En utilisant cette mesure, en théorie, un observateur pourrait déterminer la hauteur avec une précision de 0,2 milles marins, étant donné que 1 mille marin correspond à 1 minute d’arc de grand cercle.
Cela équivaut à environ 350 mètres. Cependant, dans la pratique, les navigateurs obtiennent généralement une précision de l’ordre de 1 à 2 milles marins en raison de divers facteurs. Parmi ces facteurs, on peut citer les mouvements du navire, les vagues, la netteté variable de l’horizon, les imprécisions liées à la mesure du temps ou à l’estime entre les prises de vue successives d’un même astre ou de différents astres.
La hauteur mesurée au sextant doit être corrigée des erreurs instrumentales et d’un certain nombre de paramètres propres à la hauteur de l’observateur au-dessus de l’eau, à la réfraction astronomique et à l’astre observé.