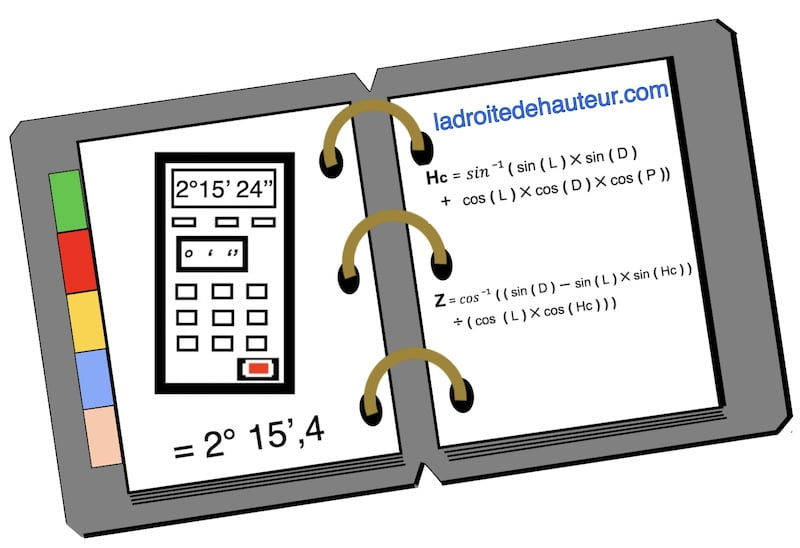
Le système sexagésimal dans la navigation maritime: on travail avec degrees, minutes et dixième de minutes!

Exemple: 17°33′,6
Donc dix-sept degrés et trente-trois virgule six minutes.


Voir aussi: formules de navigation maritime à 360° près
Une calculatrice scientifique est très utile pour résoudre les équations trigonométriques. Attention qu’il soit en mode degré (D) et qu’il contient le bouton [D M S] ou [° ‘ “]
Exemple Notation: 24°45′,5
Et non: 24° 45′ 30′′ (degrés/minutes/secondes)
Et non: 24,75833 (degrés décimaux)

Le système sexagésimal dans la navigation maritime: exemple dans le système sexagésimal et comment utiliser la calculatrice
Pour calculer K
K = arcsin( sin (24°15’,6 ) ✕ cos (42°45’,2 ) )
K = arcsin(sin ( 24[ ° ‘ ‘’ ]15,6[ ° ‘ ‘’ ] )
✕ cos ( 42[ ° ‘ ‘’ ]45,2 [ ° ‘ ‘’ ] ))
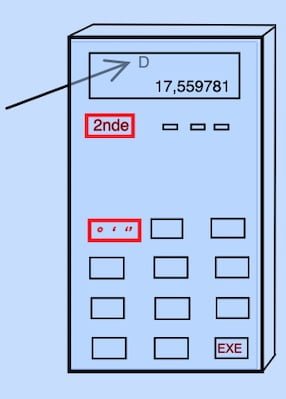
La calculatrice nous donne K = 17,559781 (décimale)
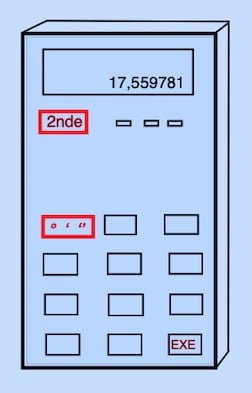
[ 2nde ] [ ° ‘ ‘’ ] donne 17° 33′ 35,21′′ (degrés/minutes/secondes)

Ensuite, à nous de transformer en degrés, minutes et dixièmes de minute.
k = 17°33′,6
Donc dix-sept degrés et trente-trois virgule six minutes.
Comment arrondir les secondes ?
60 » = 1′ ( 60secondes égale 1 minute )
| 10°10’ 06’’ | ⇨ 10°10’,1 |
| 10°10’ 12’’ | ⇨ 10°10’,2 |
| 10°10’ 18’’ | ⇨ 10°10’,3 |
| 10°10’ 24’’ | ⇨ 10°10’,4 |
| etc… | |
| 10°10’ 26, 28’’ | ⇨ 10°10’,4 |
| 10°10’ 27, 00’’ | ⇨ 10°10’,5 |
| 10°10’ 27, 31’’ | ⇨ 10°10’,5 |
| 10°10’ 30, 00’’ | ⇨ 10°10’,5 |
| etc… |
Même si l’on se trompe d’un dixième de minute, ce n’est pas si grave.

Un héritage des civilisations anciennes
Le système sexagésimal est un système de numération utilisé dans de nombreuses cultures anciennes et actuelles, notamment dans la mesure du temps et des angles. D’abord, il est basé sur le nombre 60, utilisé comme base pour représenter les nombres.
Le système sexagésimal est largement utilisé aujourd’hui dans divers domaines, notamment dans l’astronomie, la navigation, la géographie et l’horlogerie. Cependant, dans la plupart des applications courantes, le système décimal (base 10) est utilisé, car il est plus adapté aux calculs numériques et aux représentations digitales.