
Explication et deux exemples concrets.
Introduction
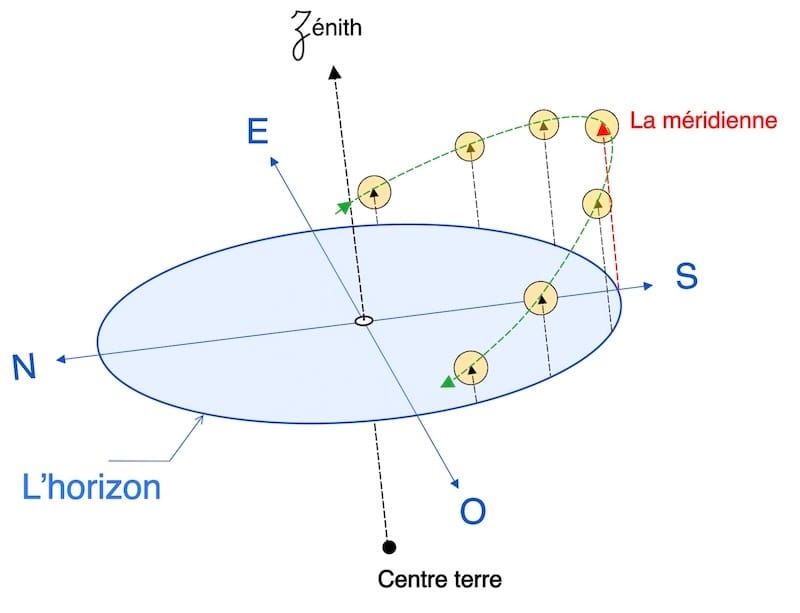

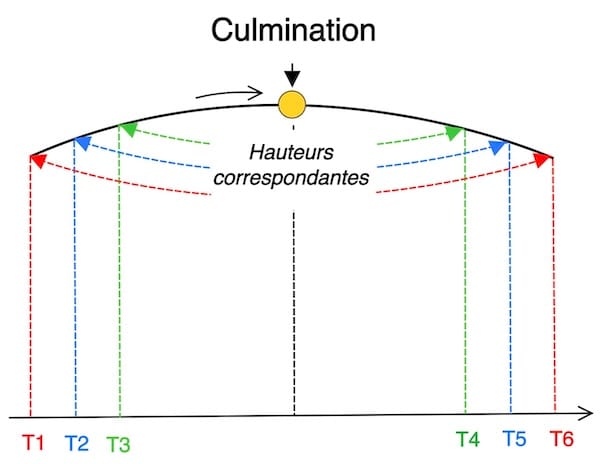
Si le Soleil culmine suffisamment haut, il est possible de déterminer sa position en effectuant trois observations : juste avant, au moment, et juste après son passage au méridien supérieur. Cette procédure repose sur deux actions distinctes.
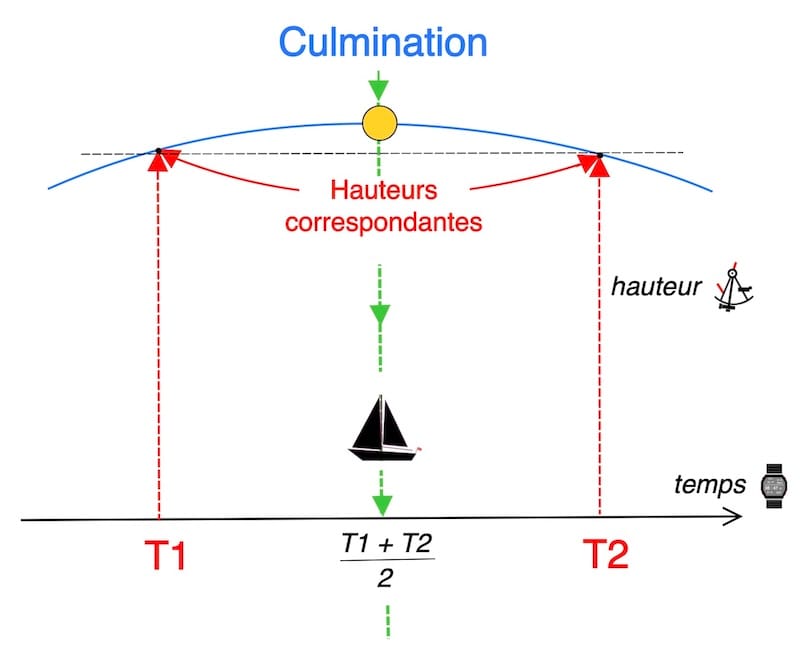
La première consiste à mesurer deux hauteurs identiques du Soleil, l’une avant et l’autre après son passage au méridien, chacune associée à l’heure exacte de l’observation.
Ces observations, appelées hauteurs égales — ou hauteurs circumzénithales correspondantes — permettent de déterminer avec précision l’heure exacte du point de culmination du soleil et donc d’en déduire la longitude, à l’aide des éphémérides nautiques.
La seconde consiste à observer le Soleil à son culminant méridien, afin d’obtenir la latitude selon la méthode classique, déjà présentée sur la page latitude méridienne.
On peut se demander pourquoi on ne prend pas l’heure exacte au moment de la culmination du Soleil.
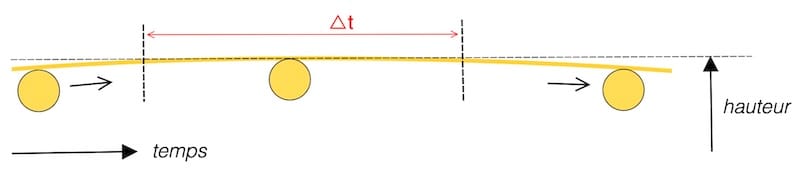
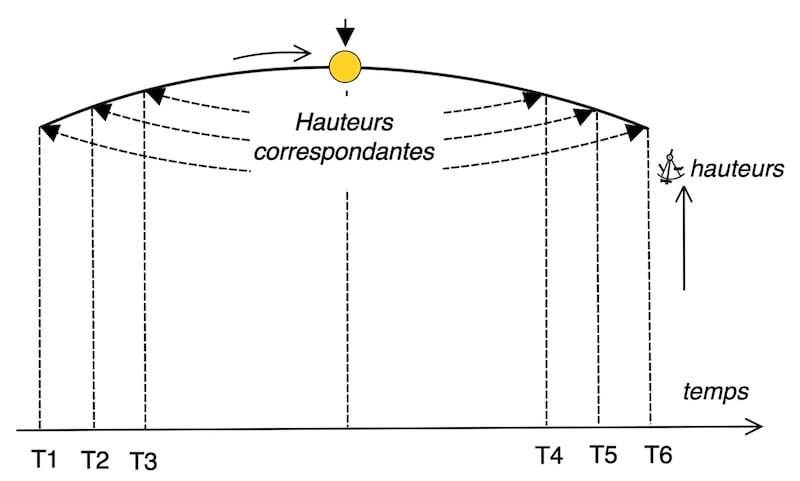
La figure montre que la mesure de la hauteur maximale ne pose pas de difficulté, mais que la détermination de l’instant précis de la culmination est impossible à l’intérieur de l’intervalle Δt : la variation de hauteur y est trop faible pour permettre une datation fiable.

Pour la méthode des hauteurs égales, il est conseillé de réaliser plusieurs séries de mesures lorsque la visibilité est réduite (brume, houle, horizon incertain), afin d’augmenter les chances d’obtenir des couples de hauteurs identiques exploitables.
Avantages et limites pratiques
Bien que cette méthode soit utilisée surtout sous les tropiques, où le Soleil culmine généralement assez haut — idéalement à des hauteurs de 78° ou plus — on peut également l’appliquer à des latitudes un peu plus élevées, à condition que le Soleil atteigne au moins 60° de hauteur.
La méthode des hauteurs égales n’est précise que si la trajectoire du Soleil est suffisamment symétrique autour de son point de culmination, ce qui suppose une hauteur de culmination élevée et des observations proches du midi apparent. Aux fortes culminations, la hauteur varie rapidement et l’instant d’observation est bien défini ; aux culminations plus basses, la variation est lente et le repérage temporel devient incertain. La méthode est donc surtout fiable sous les latitudes tropicales.

Fondamentaux de la méthode des hauteurs égales
La méthode des hauteurs égales est d’une grande simplicité : puisque les erreurs instrumentales du sextant s’annulent — les deux observations étant faites à la même hauteur, l’une avant et l’autre après le point de culmination — il n’est pas nécessaire de corriger l’erreur propre de l’instrument. Les mesures ne servent qu’à comparer deux hauteurs identiques ; l’élément essentiel réside donc dans l’heure exacte à laquelle ces deux observations sont réalisées.
En revanche, la méthode permet d’obtenir, avec une remarquable précision, l’heure du point de culmination du Soleil, ce qui en fait un excellent moyen de vérifier le chronomètre (ou la montre). Elle offre également, à partir de cet instant, la possibilité de déterminer la longitude à l’aide des éphémérides nautiques, moyennant une correction tenant compte du déplacement du navire entre la culmination et son passage au méridien.
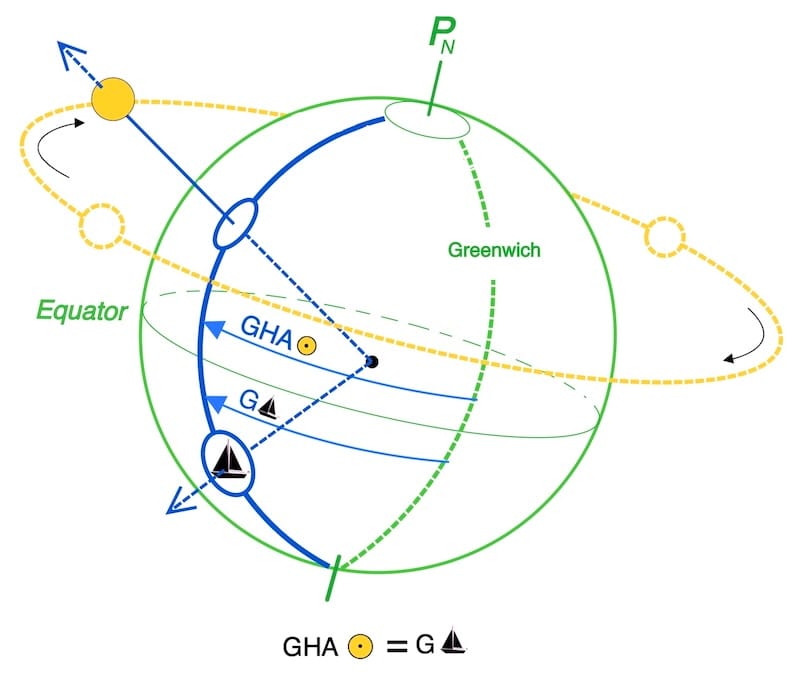
Le passage au méridien du navire peut être décalé en raison du mouvement du navire et nécessite alors une correction pour le calcul de la longitude.
Bien que simple et précise sur le plan théorique, la méthode des hauteurs égales reste longue à mettre en œuvre et exige de l’expérience : il faut maîtriser à la fois les mesures et le contrôle des temps d’observation, tout en tenant compte du déplacement du navire, qui impose ensuite des corrections supplémentaires.
Elle demeure ainsi un excellent outil pédagogique pour l’apprentissage de l’astronavigation, plutôt qu’une méthode réellement opérationnelle en navigation.
Mais par mer calme et ciel dégagé, l’expérience peut se révéler très satisfaisante… et tant pis pour l’apéro !
Mise en œuvre des observations
L’observateur mesure deux hauteurs égales du Soleil :
– l’une avant le point de culmination (avant le midi apparent),
– l’autre après le point de culmination (après le midi apparent).
Ces deux hauteurs étant égales, le Soleil est symétriquement disposé de part et d’autre de son point de culmination. Le milieu de temps entre les deux instants d’observation correspond alors à l’instant du midi apparent local. On suppose, pour l’instant, que la position du navire est restée inchangée.

En pratique, on ne se limite pas à deux observations. On relève plusieurs hauteurs du Soleil avant et après le point de culmination — en général trois à six mesures de chaque côté — afin d’obtenir plusieurs paires de hauteurs égales.
Chaque paire donne un instant d’égalité de hauteur. En prenant la moyenne de ces instants, on obtient avec plus de précision l’heure du point de culmination du Soleil (midi apparent local).
latitude méridienne
En observant la hauteur maximale du Soleil au point de culmination, on peut calculer la latitude méridienne. Cette démarche est indépendante de la méthode des hauteurs égales.
Longitude méridienne
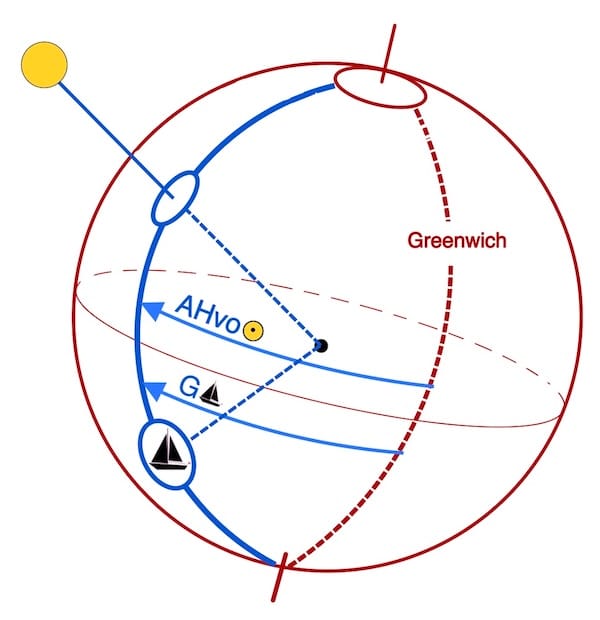
Au moment (T1+T2)/2 en heure TU, on obtient l’angle horaire à Greenwich du Soleil à l’instant de sa culmination. Cette valeur doit ensuite être corrigée pour déterminer l’angle horaire correspondant à son passage au méridien du navire, et donc la longitude.
Les éphémérides astronomiques sont publiées en France dès 1679 avec La Connaissance des Temps, notamment grâce aux travaux de l’abbé Picard.
Le GHA, en tant que donnée normalisée pour la navigation maritime, apparaît avec le British Nautical Almanac à partir de 1767.
Règles pour convertir AHvo (GHA) en longitude
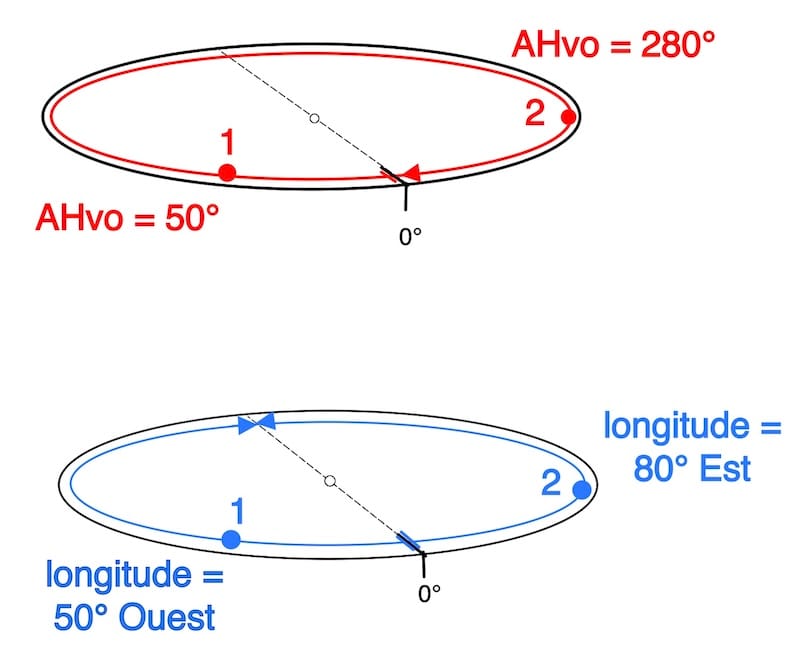
Rappel: les angles horaires vont de 0 à 360° vers l’ouest
Or pour les coordonnées sur terre on utilise longitude Est (0° à 180°) et longitude Ouest de (0° à 180° )

Ainsi :
Si AHvo < 180°
⇒ Longitude Ouest = AHvo
Si AHvo > 180°
⇒ Longitude Est = 360° − AHvo
Cadence d’observation avant et après culmination
Le tableau ci-dessous présente des indications pratiques sur la durée utile des observations, établies en fonction de la hauteur estimée du Soleil au moment de sa culmination.
Ces indications, tirées de l’ouvrage de référence qu’est le Traité de navigation, supposent que l’on effectue trois séries successives de mesures de hauteur.
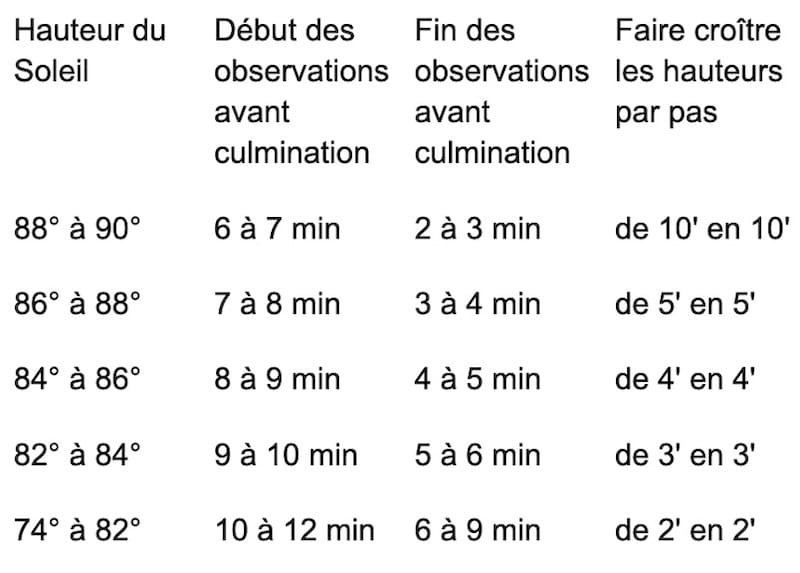
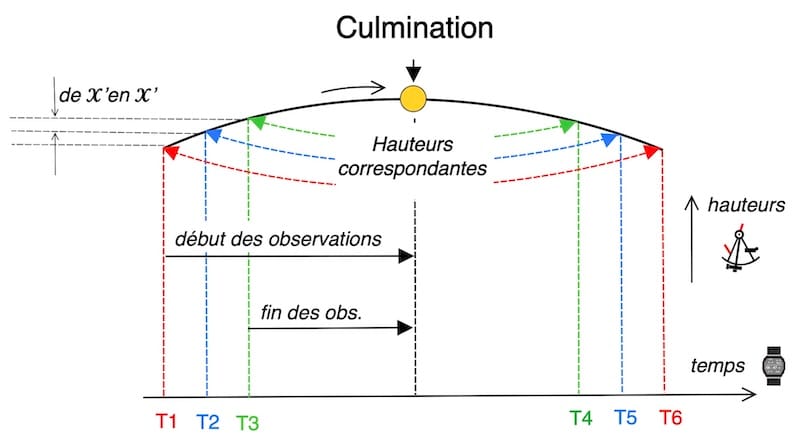
Tableau des observations
| Hi | TU ( h m s) | |
| avant T1 | ||
| avant T2 | ||
| avant T3 | ||
| Observation à la culmination (latitude méridienne) | ———— | |
| après T4 | ||
| après T5 | ||
| après T6 |

Il suffit ensuite de lire dans les éphémérides l’AHvo du Soleil correspondant à cette heure moyenne en TU, qui est celle du point de culmination. Cette valeur doit ensuite être corrigée pour obtenir l’angle horaire du Soleil lors de son passage au méridien du navire, et donc la longitude.
Pourquoi une correction de mouvement du navire ?
Les mouvements non purement est–ouest modifient la symétrie des hauteurs égales, car ils entraînent une variation de latitude du navire et, par conséquent, de l’altitude apparente du Soleil. L’importance de cette correction due aux déplacements nord–sud dépend de la différence entre la latitude et la déclinaison, et devient d’autant plus notable que la vitesse est élevée.
Formule générale de correction
Formule de la correction à apporter (Δλ) — résultat en minutes d’arc
Δλ = (12/π) × Vf × cos Rf × (tan D – tan L)
où :
– Vf = vitesse fond du navire (en nœuds)
– Rf = route fond
– L = latitude du navire
– D = déclinaison du Soleil
La correction est nulle
La correction devient nulle lorsque :
– le navire est immobile (V = 0),
– la route est est–ouest (cos Rf = 0),
– la latitude = déclinaison.
Interprétation du signe de Δλ
Le signe de la correction Δλ dépend entièrement du sens du déplacement du navire et de la position du Soleil par rapport à la latitude.
Δλ = (12/π) × Vf × cos Rf × (tan D − tan L)
Ainsi, le signe de Δλ est déterminé par le produit, qui peut être positif ou négatif.
On applique ensuite la formule :
AHvo corrigé = AHvo − Δλ
Cette expression est valable dans tous les cas, sans distinction d’hémisphère ni de saison, à condition de conserver le signe réel de Δλ donné par la formule.
Tableau simplifié de correction de mouvement du navire
Pour simplifier l’usage de cette formule un peu lourde, un tableau est fourni. Il permet d’obtenir le même résultat, avec toutefois une précision légèrement moindre en raison des arrondis. Ce tableau téléchargeable est accompagné de six exemples d’utilisation.
Explication complémentaire
Se rapprocher du Soleil (le Soleil monte)
→ le navire va vers la déclinaison du Soleil
→ le midi vrai arrive plus tôt
→ l’angle horaire du Soleil diminue
S’éloigner du Soleil (le Soleil descend)
→ le navire s’éloigne de la déclinaison du Soleil
→ le midi vrai arrive plus tard
→ l’angle horaire du Soleil augmente

Exemple 1 : Latitude méridienne et, indépendamment, longitude par la méthode des hauteurs égales du Soleil.
Le 19 août 2025 à 01 00 TU (T1) on a le point estimé:
06° 33.7 N; 129° 36.6 E
Rf = 210° ; Vf = 10 noeuds
Tcf = TU − f = 01h 00 − ( − 9) = 10 h 00
Calculer la latitude et longitude au moment de la méridienne
Préparation avant les observations
1) Calcul de l’heure méridienne approximative:
2) Calcul de la hauteur approchée au moment de la méridienne
3) Utilisation du tableau “Cadence d’observation avant culmination (méthode des égales hauteurs)” avec l’heure et la hauteur approximatives calculées auparavant
Observations
4)
| Hi | TU ( h m s) | |
| avant T1 | ||
| avant T2 | ||
| avant T3 | ||
| Observation à la culmination (latitude méridienne) | ———— | |
| après T4 | ||
| après T5 | ||
| après T6 |
Calcul final
5 )Calcul de la latitude méridienne:
6) Calcul de l’heure du point de culmination
7) Calcul de la longitude au moment de la méridienne:

1) Calcul de l’heure méridienne approximative:
On commence par calculer l’heure méridienne approximative comme expliqué sur la page “Navigation astronomique: calculer l’heure méridienne”
19 août 2025 (Les éphémérides nautiques)
| TU | AHvo | D |
| 00 | 179° 04.6’ | 12° 45.3’ N |
| 01 | 194° 04.8’ | 12° 44.5’ N’ |
| 02 | 209 °04.9’ | 12° 43.7’ N |
calcul: AHvg = AHvo + G (Est)
| AHvo = 194° 04.8’ | 01 00 TU (T1) |
| G = 129° 36.6’ | |
| ______________ + | |
| AHvg = 323° 41.4’ | |
| P = 36° 18.6’ |
Le calcul de l’angle polaire (P) constitue l’élément central de l’exercice principal proposé sur ladroitedehauteur.com.
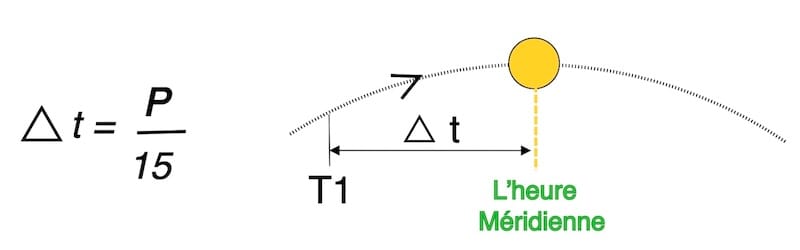
△t = P ÷ 15
△t = 36° 18.6’ ÷ 15 = 2 h 25 m 14 s
L’heure méridienne approximative :
T1 + △t = 01 h 00 + 2 h 25 = 03 h 25 TU
2) Calcul de la hauteur approchée au moment de la méridienne
h = 90° − ∣ L − D ∣
∣L−D∣ : il s’agit tout simplement de la différence entre la latitude estimée (L) et la déclinaison (D) du Soleil, prise en valeur absolue.
Latitude(L) à 03 h 25 TU ≈ 6° 10’ N (Estime pris sur la carte)
Déclinaison(D) à 03 h 25 TU ≈ 12° 42.5’ N
19 août 2025 (Les éphémérides nautiques)
| TU | AHvo (GHA) | D |
| 03 | 224°05.1’ | 12°42.9’ N |
| 04 | 239°05.2 | 12°42.0’ N |
∣ L − D ∣ = ∣ 6° 10’ N − 12° 42.5’ N ∣
= ∣ – 6° 10’ ∣ ⇒ 6° 32.5’ (valeur absolue)
la hauteur approchée au moment de la méridienne:
h = 90° − ∣ L − D ∣
⇒ 90° − 6° 32.5’ = 83° 27.5’
3) Utilisation du tableau : Cadence d’observation avant et après culmination

La hauteur calculée au point 2 est d’environ 83°.
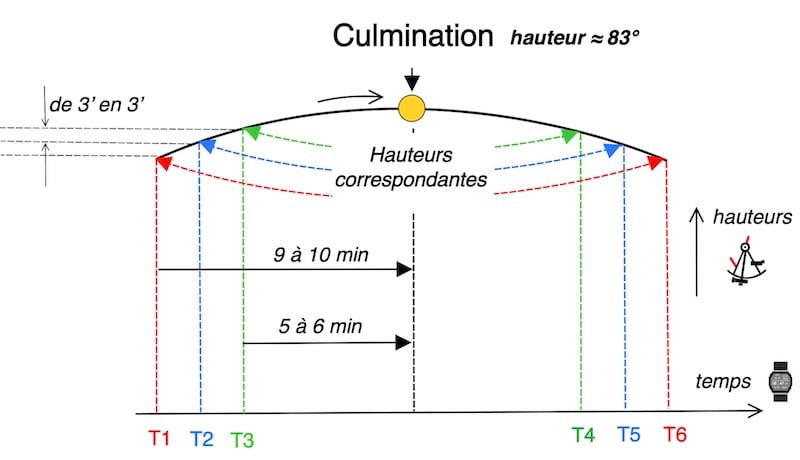
Donc d’après le tableau on commence approximativement 9 / 10 minutes avant et fin d’observation 5 / 6 minutes avant la culmination l’application de cette tableau ne demande pas un rigueur absolu mais c’est une bonne indication.
4) Les observations
| Hi | TU ( h m s) | |
| avant T1 | 82° 49.3’ | 03 15 11 |
| avant T2 | 82° 52.3’ | 03 15 43 |
| avant T3 | 82° 55.3’ | 03 16 18 |
| Observation à la culmination (latitude méridienne) | 83°19.2’ | ≈ 03 26 |
| après T4 | 82° 55.3’ | 03 35 17 |
| après T5 | 82° 52.3’ | 03 35 53 |
| après T6 | 82° 49.3’ | 03 36 28 |
5) Calcul de la latitude méridienne:
Une fois rempli le tableau on range le sextant et on commence à calculer la latitude méridienne
Calcul de la méridienne:

La déclinaison (D), obtenue dans les éphémérides nautiques quotidiennes, est positive au Nord et négative au Sud.
La distance zénithale (α) est prise positive lorsque le soleil est observé au Sud à l’heure de la méridienne, et négative lorsque le soleil est observé au Nord.
Hi = 83° 19.2’ au moment méridienne
collimation ℇ = ⎼2.2’
hauteur l’oeil = 4m
Calcul Hv:


| Hi | 83° 19.2’ |
| ℇ | ⎼ 2.2’ |
| ________ + | |
| Ho | 83° 17’ |
| 1re correction | 12.4’ |
| 2e correction | ⎼ 0.2’ |
| _________ + | |
| Hv | 83° 29.2’ |
𝛂 = 90° − Hv = 90° − 83°29.2’ = 06°30.8’ (négatif car Soleil au Nord)
L méridienne = D + 𝜶 :
12°42.5’ + ( − 06°30.8’) = 06° 11.7’ Nord
6) Calcul de l’heure du point de culmination
Chaque paire d’altitudes égales définit un intervalle de temps symétriquement réparti autour du midi apparent local. Le milieu temporel entre les deux observations correspondantes constitue donc une estimation de l’instant du point de culmination du Soleil.
Lorsque plusieurs paires d’altitudes égales sont disponibles, l’instant exact du point de culmination du Soleil est obtenu en faisant la moyenne des instants d’observation de toutes les visées effectuées avant et après la culmination. Cette moyenne permet de réduire les erreurs aléatoires d’observation et d’améliorer la précision du résultat.
(T1 + T2 + T3 + T4 + T5 + T6) / 6
= 03 25 48 (TU)
7) Calcul de la longitude au moment méridienne:
À partir de cette heure moyenne, on relève dans les éphémérides l’AHvo du Soleil correspondant à l’instant de la culmination. Cette valeur doit ensuite être corrigée pour tenir compte du déplacement du navire, afin d’obtenir la longitude.
19 août 2025 (Les éphémérides nautiques)
| TU | AHvo | D |
| 03 | 224°05.1’ | 12°42.9’ N |
| 04 | 239°05.2 | 12°42.0’ N |
| TU | AHvo (GHA) |
| 03 00 00 | 224° 05.1’ |
| * increment 00 25 48 + | 6° 27’ + |
| 03 25 48 | 230° 32.1’ |
* 00 h 25 m 48 s × 15° = 6° 27′
Si la vitesse du bateau a été nulle :
AHvo = 230°32.1’
Mais on doit appliquer la correction :
Δλ = (12/π) × Vf × cos Rf × (tan D – tan L)
Δλ = (12/π) × 10 × cos 210° × ((tan 12°42.5’) − (tan 6°11.7’))
⇒ Δλ = ⎼ 3.9’
AHvo = AHvo − Δλ’
= 230°32.1’ − (−3.9)’ = 230°36.0’
Si AHvo < 180° ⇒ Longitude Ouest = AHvo
Si AHvo > 180° ⇒ Longitude Est = 360° − AHvo
AHvo > 180° ⇒ 360° − 230° 36.0′ = 129° 24.0′
Longitude G méridienne :
G méridienne = 129°24.0 E

Exemple 2 : Latitude méridienne et, indépendamment, longitude par la méthode des hauteurs égales du Soleil.
exemple 2: Le 14 décembre 2025 à 21 00 TU (T1) on a le point estimé:
38°37.6′ S; 160°32.5′ O.
Rf = 040° ; Vf = 11 noeuds
Tcf = TU − f = 21h 00 − ( + 11) = 10 h 00
1) Calcul de l’heure méridienne approximative:
14 décembre 2025 (Les éphémérides nautiques)
| TU | AHvo | D |
| 21 00 00 | 136° 16.0 | S 23° 15.6 |
| 22 00 00 | 151° 15.7 | S 23° 15.7 |
| 23 00 00 | 166° 15.4 | S 23° 15.9 |
AHvo = 136° 16′ 21 00 TU (T1)
G = 160° 32.5′ O (par soustraction)
AHvg = 335° 43.5′
P = 24°16.5′
△t = P / 15
△t = 24° 16.5′ / 15 ≈ 1 h 37
L’heure méridienne approximative :
T1 + △t = 21 h 00 + 01 h 37 = 22 h 37 TU
⇒ 11 h 37 Tcf
2) Calcul de la hauteur approchée au moment de la méridienne
Latitude (L) à 22 h 37 TU : ≈ 38°24′ S (estime prise sur la carte)
Déclinaison (D) à 22 h 37 TU : ≈ 23°16′ S
La formule :
h = 90° − |L − D|
On calcule la différence :
|L − D| =| ⎼ 38° 24’ − ( −23° 16′) | |L − D| = 15°08′ (toujours positive)
Donc hauteur approximative du Soleil au passage au méridien: h = 90° − 15°08′ = 74°52′
3) Utilisation du tableau : Cadence d’observation avant et après culmination
Cadence d’observation avant culmination (méthode des égales hauteurs)”
(Rappel du tableau)
| Hauteur du Soleil | Début des observations avant culmination | Fin des observations avant culmination | Faire croître les hauteurs par pas |
| 88° à 90° | 6 à 7 min | 2 à 3 min | de 10′ en 10′ |
| 86° à 88° | 7 à 8 min | 3 à 4 min | de 5′ en 5′ |
| 84° à 86° | 8 à 9 min | 4 à 5 min | de 4′ en 4′ |
| 82° à 84° | 9 à 10 min | 5 à 6 min | de 3′ en 3′ |
| 74° à 82° | 10 à 12 min | 6 à 9 min | de 2′ en 2′ |
4) Les observations
| Hi | TU ( h m s) | |
| avant T1 | 74 20.9 | 22 23 44 |
| avant T2 | 74 22.9 | 22 24 32 |
| avant T3 | 74 24.9 | 22 25 30 |
| Observation à la culmination (latitude méridienne) | 74°36.8 | ≈ 22 37 |
| après T4 | 74 24.9 | 22 48 18 |
| après T5 | 74 22.9 | 22 49 13 |
| après T6 | 74 20.9 | 22 50 07 |
5) Calcul de la latitude méridienne :
Hi = 74°36.8′ au moment méridienne
collimation ℇ = 2.0′
hauteur l’oeil = 3 m
| Hi | 74° 36.8’ |
| ℇ | 2.0’ +________ |
| Ho | 74° 38.8’ |
| 1re corr. | 12.7’ |
| 2e corr. | 0.3’ +________ |
| Hv | 74° 51.8’ |
𝜶 = 90° − Hv = 90° − 74° 51.8′
= 15°08.2′ (négatif car Soleil au Nord)
L méridienne = D + 𝜶
= − 23 15.8′ + ( − 15°08.2’) = 38° 24′ Sud
6) Calcul de l’heure du point de culmination
(T1 + T2 + T3 + T4 + T5 + T6) / 6
= 22 h 36 m 54 s TU
On obtient ainsi l’heure exacte du point de culmination du Soleil, utilisée comme base pour le calcul de la longitude.
7) Calcul de la longitude au moment méridienne :
14 décembre 2025 (éphémérides nautiques)
| TU | AHvo | D |
| 21 00 00 | 136° 16.0′ | S 23° 15.6′ |
| 22 00 00 | 151° 15.7′ | S 23° 15.7′ |
| 23 00 00 | 166° 15.4′ | S 23° 15.9′ |
| TU | AHvo (GMT) |
| 22 00 00 | 151°15.7’ |
| ** increment 00 36 54 + | 9°13.5’ |
| 22 36 54 | 160°29.2’ |
** 00 h 36 m 54 s × 15° = 9° 13.5′
Si la vitesse du bateau a été nulle:
longitude = AHvo = 160°29.2
Mais on doit appliquer une correction pour la déplacement du navire
Δλ = (12/π) × Vf × cos Rf × (tan D – tan L)
Δλ = (12/π) × 11 × cos 040° × ((tan − 23° 15.8′) − (tan −38°24′))
Δλ = 11.7′
AHvo corrigé = AHvo − Δλ
AHvo corrigé = 160°29.2′ − 11.7′ = 160°17.5′
Si AHvo < 180° ⇒ Longitude Ouest = AHvo
Si AHvo > 180° ⇒ Longitude Est = 360° − AHvo
Longitude G méridienne :
AHvo < 180° ⇒ G méridienne = 160°17.5′ O