
comprendre LE PRINCIPE de la droite de hauteur (La méthode Marcq Saint-Hilaire)
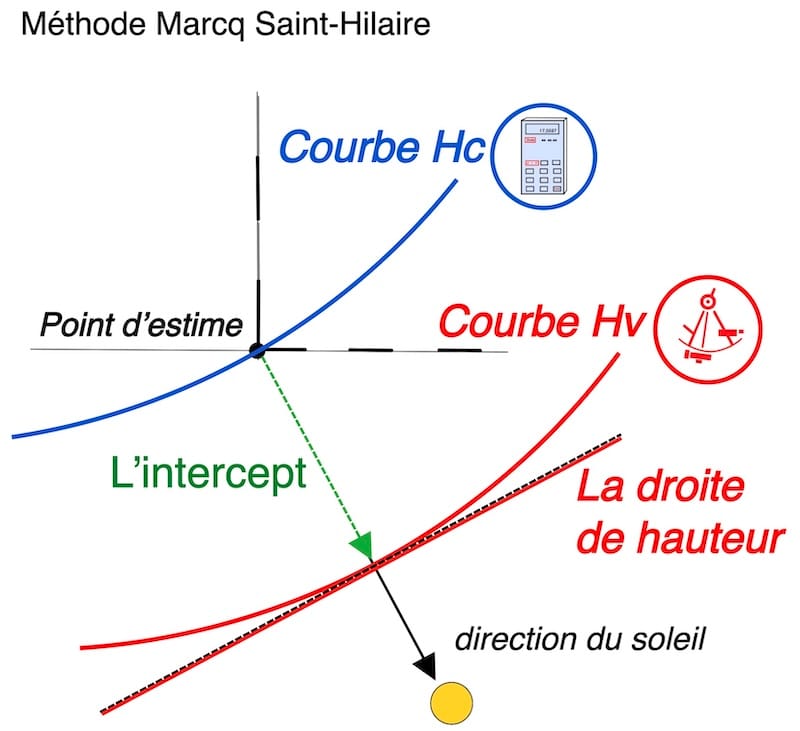
La méthode compare deux méthodes indépendantes:
1 la mesure au sextant (Hv)
2 le calcul impliquant la position estimée (Hc).
Cette dernière est utilisée comme référence pour tracer une courbe (Hv) sur une carte nautique, présentant cette courbe localement comme une ligne droite.

La méthode Marcq Saint – Hilaire implique la comparaison entre deux méthodes entièrement différentes :
1) Mesurer avec le sextant pour trouver le cercle de hauteur vraie (Hv.)
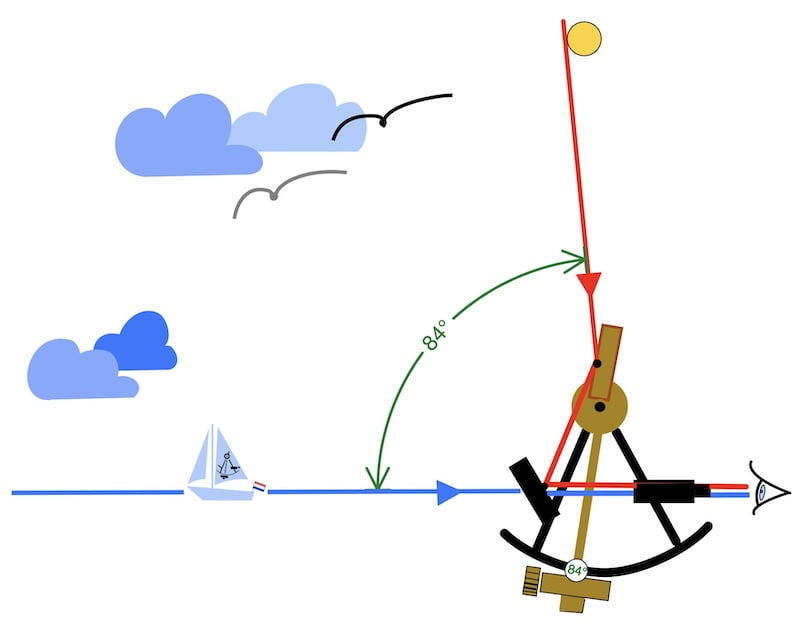
À ce stade, une brève parenthèse sur la position géographique (Pg) s’impose afin de mieux comprendre la suite des explications.
Quelle est la Position Géographique (Pg) d’un Astre ?
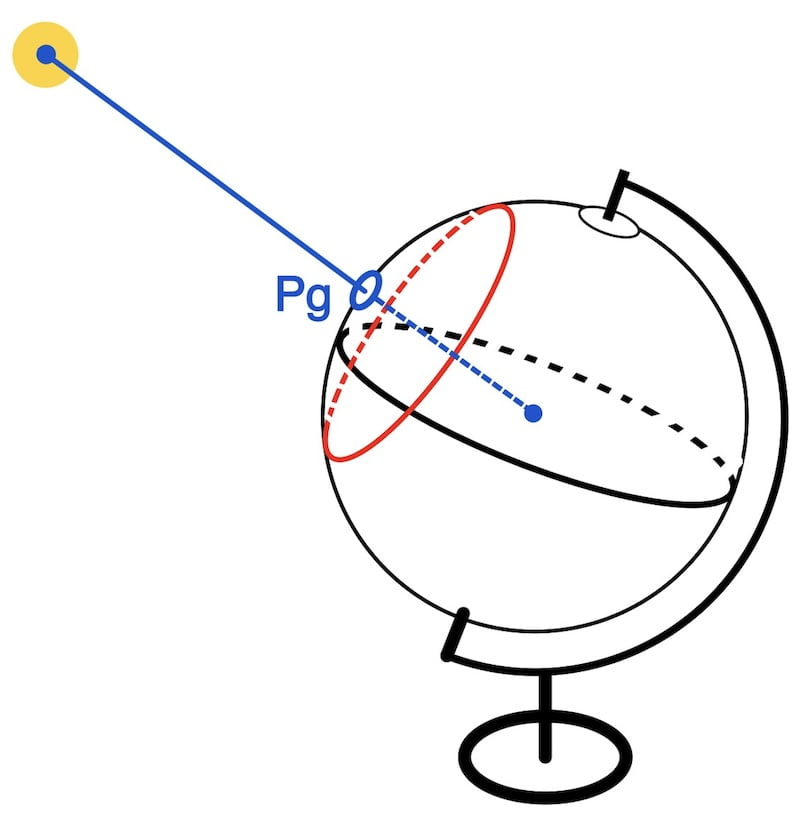
La Position Géographique (Pg) est le point à la surface de la Terre où un astre (comme le Soleil, la Lune ou une étoile) se trouve exactement au zénith — c’est-à-dire à 90° d’altitude.
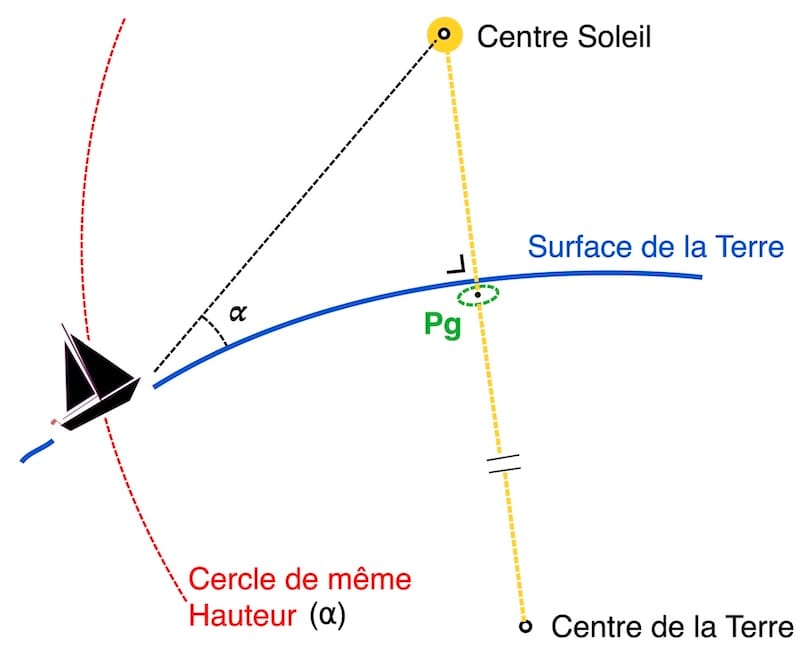

Pourquoi est-ce important en navigation astronomique ?
La Pg est le centre du cercle de position, aussi appelé cercle d’égale hauteur.
Lorsque vous mesurez l’altitude d’un astre avec un sextant, vous vous situez quelque part sur ce cercle.
Ce concept permet de tracer une droite de hauteur (LOP) : un petit arc de ce cercle, reporté sur la carte.
Comment calcule-t-on la position géographique (Pg) ?
La Gp a deux coordonnées : latitude et longitude, comme n’importe quel point terrestre.
- Déclinaison (Dec)
→ Donne la latitude de la Gp
→ C’est la distance angulaire de l’astre au nord ou au sud de l’équateur céleste - Angle Horaire de Greenwich (l’AHv₀)
→ Donne la longitude de la Gp
→ Mesurée vers l’ouest à partir du méridien de Greenwich
Ces deux valeurs, la déclinaison et l’AHv₀, se trouvent dans les éphémérides nautiques pour une heure universelle (UT) ronde donnée. Il suffit ensuite d’effectuer un petit calcul pour obtenir la déclinaison (D) et l’AHv₀ à l’heure exacte.

Pourquoi bien comprendre ce cercle est essentiel
Il est fondamental de bien comprendre le cercle d’égale hauteur, car ce concept géométrique constitue la base même de la navigation astronomique.
Cela remplit deux objectifs importants :
- Comprendre en profondeur la méthode de Marcq Saint-Hilaire, qui repose entièrement sur ce principe.
- Acquérir les bases nécessaires aux calculs que vous découvrirez progressivement sur ce site.

2) Calculer, à partir de notre point d’estime, à l’aide de formules trigonométriques sphériques, le cercle de hauteur approprié (Hc).
Les conditions requises sont les suivantes : le point d’estime ne doit pas avoir une incertitude de plus de 30 à 40 milles, et l’heure de la mesure doit être égale à l’heure intégrée dans le calcul.
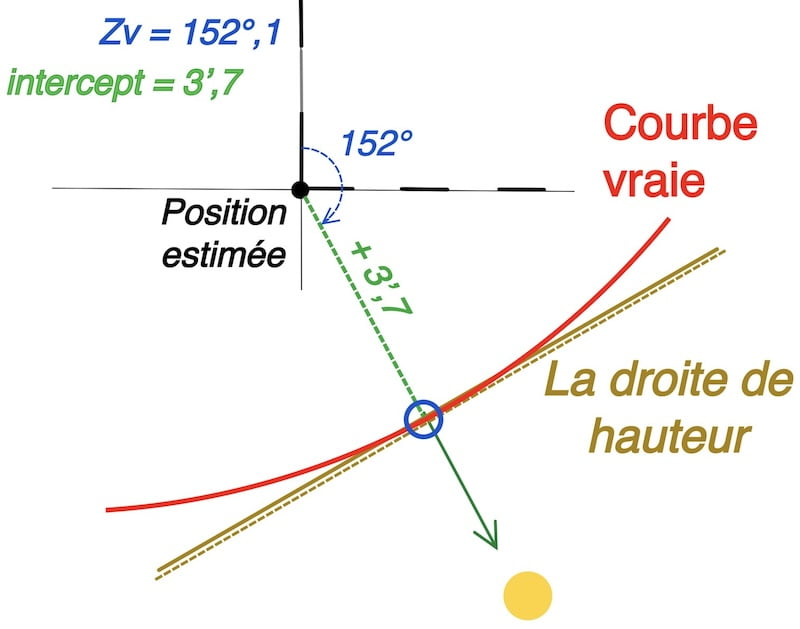
Dans ce cas, ces deux cercles sont très proches et localement assimilables à des courbes parallèles, avec une différence horizontale appelée intercept.

Puis, le point d’estime sert de point de référence pour tracer la courbe de hauteur vraie, localement associée à une droite.
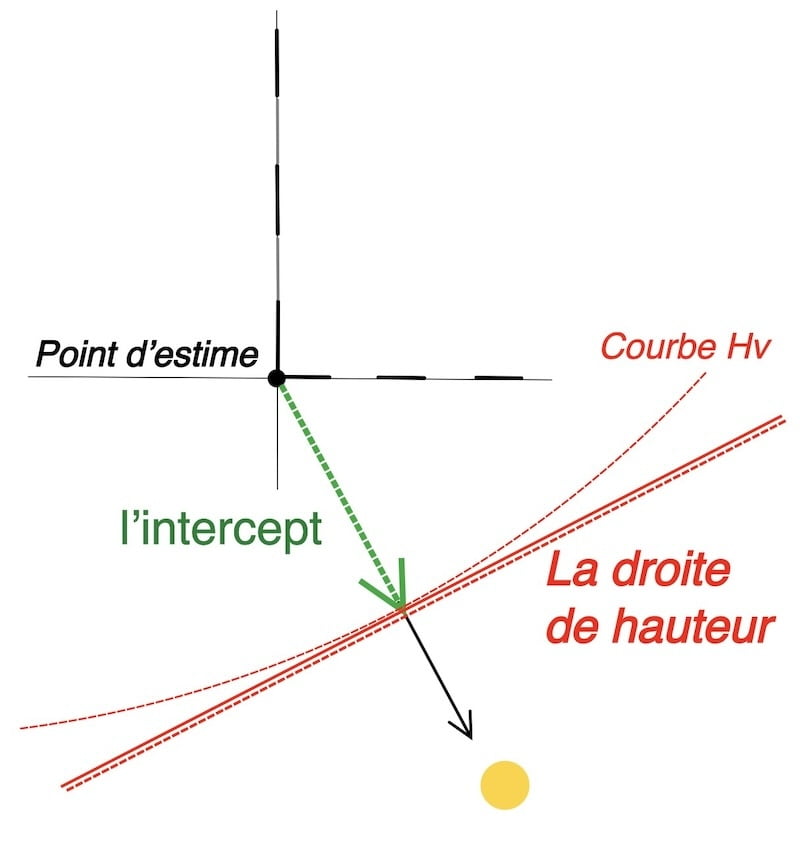
Par ailleurs, en France, cette méthode s’appelle la méthode des points rapprochés, et en anglais, elle est appelée la méthode d’intercept (the intercept method).

En résumé, la méthode, qui n’est pas purement mathématique, implique deux cercles indépendants situés étroitement l’un à l’autre avec des caractéristiques presque identiques.

Bien sûr, tout repose sur le cercle de hauteur vraie mesuré avec le sextant.
Cependant, il manque une référence utilisable, car la position géographique (PG), qui se situe au centre du cercle, est trop éloignée pour être reportée directement sur la carte.
En conclusion, le calcul du cercle (Hc) à partir du point estimé constitue notre référence et nous permet de situer la droite de hauteur obtenue par l’observation au sextant, afin de la tracer sur la carte par la suite.

LA DROITE DE HAUTEUR ou « line of position » (LOP) en anglais
Une droite de hauteur est une ligne droite marquée sur une carte nautique qui représente la position potentielle d’un navire quelque part sur cette ligne, déterminée à l’aide d’un sextant et de calculs pertinents.
Essentiellement, cela signifie que le navire est positionné quelque part le long de cette ligne, sans pour autant fournir une position exacte.
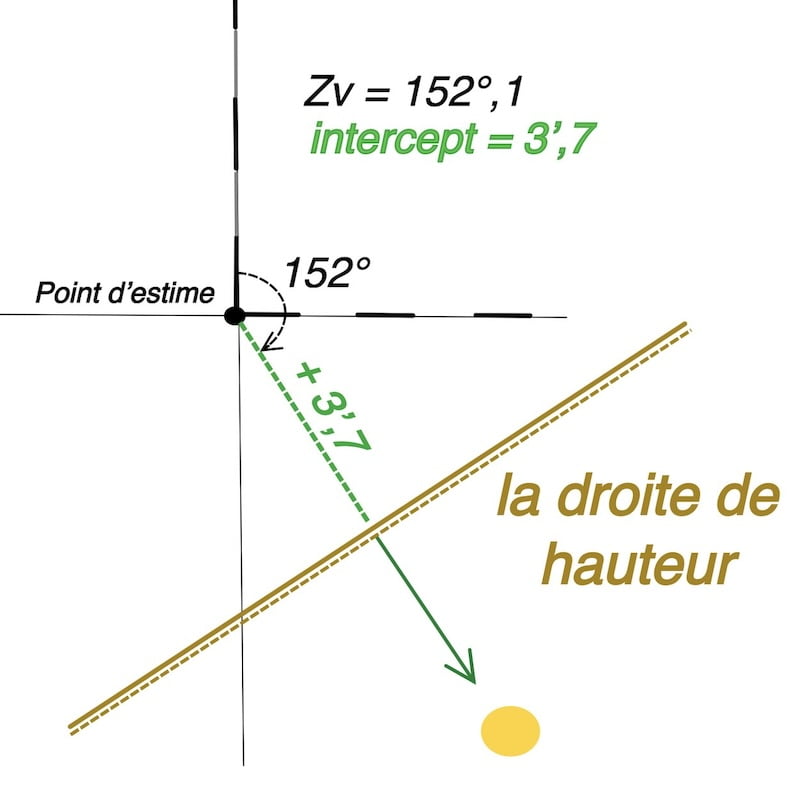
Pour déterminer avec précision la position d’un navire, il est nécessaire d’avoir les intersections d’au moins deux droites de hauteur.
Le processus implique de prendre une première observation avec un sextant pour mesurer la hauteur du soleil au-dessus de l’horizon et calculer la première droite de hauteur.

Par la suite, une deuxième observation est effectuée quelque temps plus tard alors que le soleil change son angle d’azimut lors de son mouvement d’est en ouest.
La deuxième droite de hauteur est alors calculée, et l’intersection de ces deux lignes révèle la position du navire.
Cependant, il y a plusieurs autres facteurs à prendre en compte, tels que le mouvement du navire entre les deux lignes de position.


LE PRINCIPE de la droite de hauteur en trois étapes:
1 Obtention du cercle observé (Ho) avec le sextant.
2 Calcul du deuxième cercle (Hc) à partir de la position estimée.
3 Les comparer.

Etape (1) l’observation avec le sextant


Hv (hauteur vraie)
Sur notre lieu inconnu (puisque le but est de chercher notre position) nous mesurons avec le sextant la hauteur du soleil au-dessus de l’horizon.
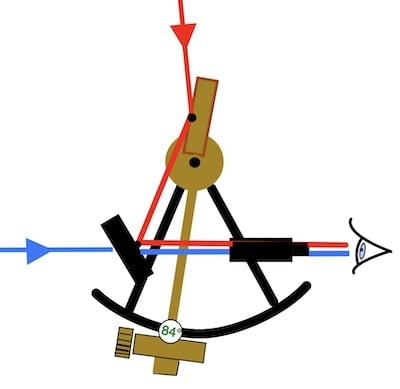

Après avoir apporté des corrections (qui seront expliquées plus tard dans la section Hv de notre page interactive), nous modifions cette hauteur comme si nous étions au centre de la Terre, et nous l’appelons la hauteur vraie (Hv).
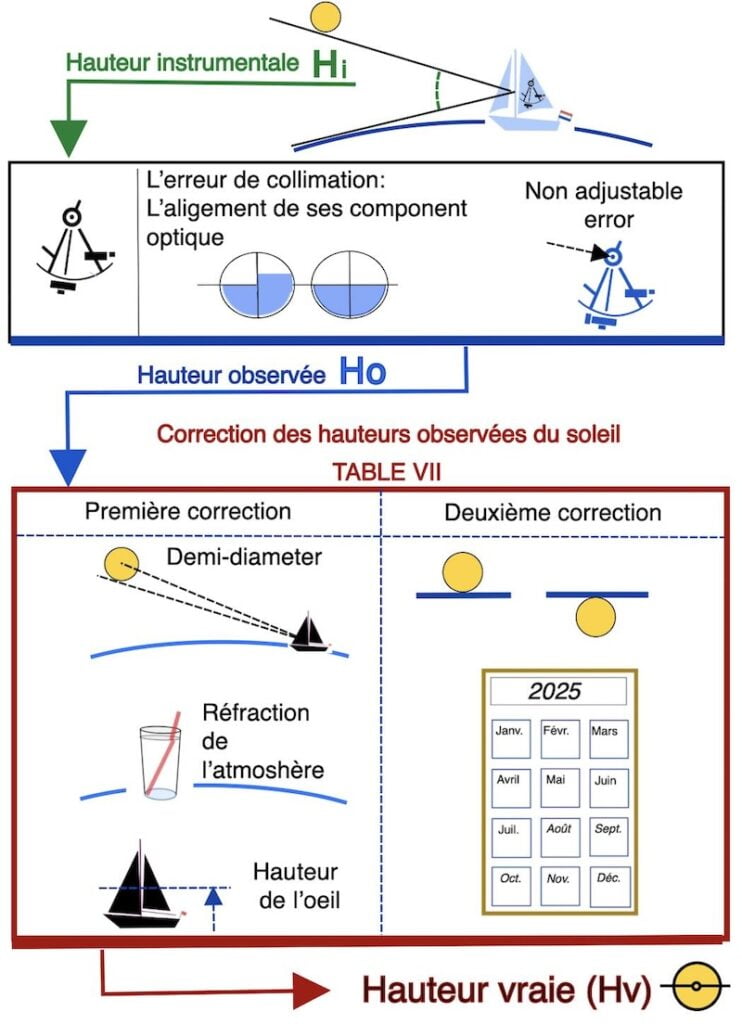
Vu l’immense distance entre la Terre et le Soleil, cette modification serait très petite et presque insignifiante.
Le sextant, pendant l’observation, est tourné vers le point Pg (direction du soleil bien sûr).

La droite de hauteur est une portion de cette immense courbe (cercle de position) que l’on assimile localement à une droite!

La droite de hauteur est donc perpendiculaire à la direction de l’astre
À ce stade, notre point d’estime n’a pas encore d’importance, autrement dit, il ne joue pas encore de rôle.
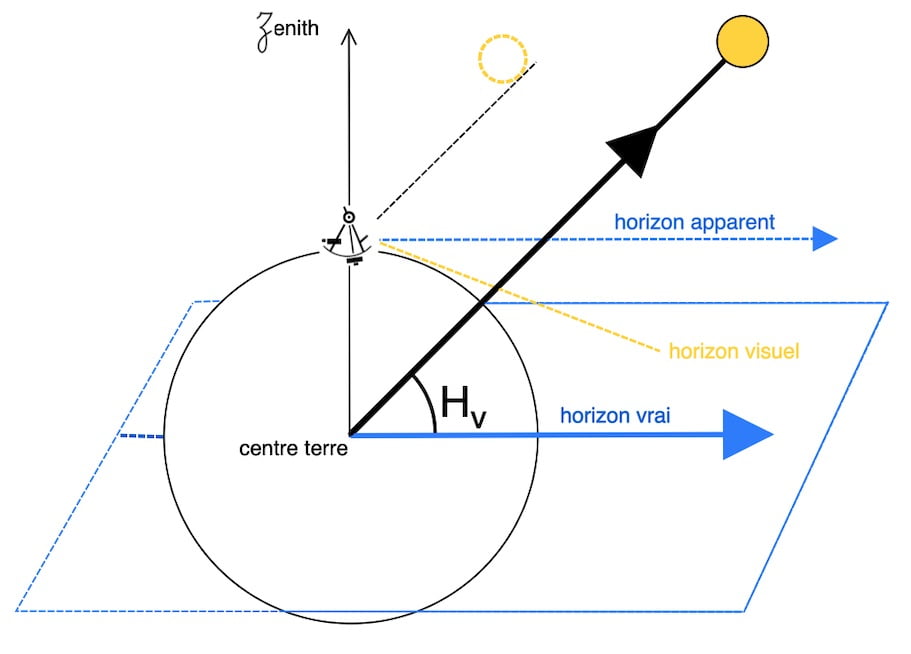
Attention: centre terre, centre soleil
Avec cette Hv, il y a une courbe de même hauteur et une droite de hauteur localement associée.

LE PRINCIPE de la droite de hauteur: étape (2) le calcul


Hc (hauteur calculée)
Sur notre point d’estime, on peut, à l’aide de l’heure exacte de l’observation, des éphémérides nautiques et des formules trigonométriques sphériques, calculer la hauteur sur le lieu d’estime, appelée hauteur calculée (Hc).

Attention : centre Terre, centre Soleil. Ces formules trigonométriques sphériques calculent toujours entre le centre Terre et les centres de tous les astres (Soleil, étoiles, Lune et planètes).
Hc possède aussi sa propre courbe de même hauteur et droite de hauteur localement associée
En même temps, on calcule également la direction de l’astre (l’azimut).


LE PRINCIPE de la droite de hauteur: étape (3) comparer Hv et Hc


Dans un premier temps, on peut dire que la hauteur vraie (Hv) est corrigée comme si l’on se trouvait non pas à la surface de la Terre, mais en son centre.
La hauteur calculée (Hc), obtenue à partir de notre point d’estime grâce aux formules trigonométriques, peut alors être comparée à Hv.

On peut estimer que la droite de hauteur Hc est parallèle à celle de Hv, puisque le lieu d’estime et le lieu d’observation sont proches et orientés vers le Soleil dans la même direction.
La distance entre les deux droites de hauteurs (qui sont donc parallèle) sur la surface de la terre s’appelle l’intercept et on adopte Hv – Hc = intercept

Avec le point d’estime sur la carte et la direction du soleil, on peut tracer la droite de hauteur (Hc) qui passe par notre point d’estime.
C’est notre référence !

Il est à noter que l’incertitude du point d’estime ne devrait de préférence pas dépasser plus ou moins 30 milles.


L’intercept:
La distance entre les deux droites de hauteurs (qui sont donc parallèle) sur la surface de la terre s’appelle l’intercept et on adopte Hv – Hc = intercept
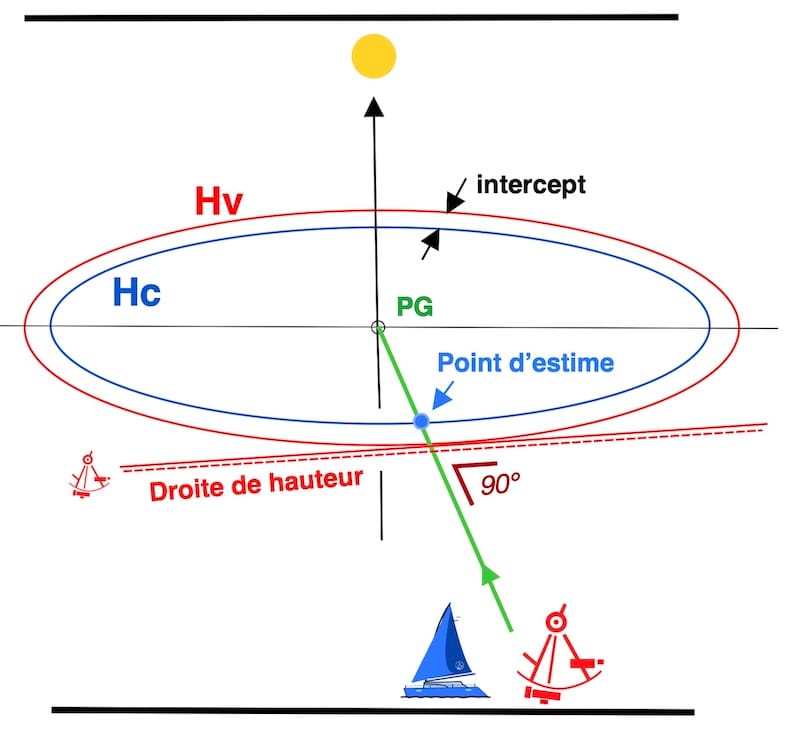
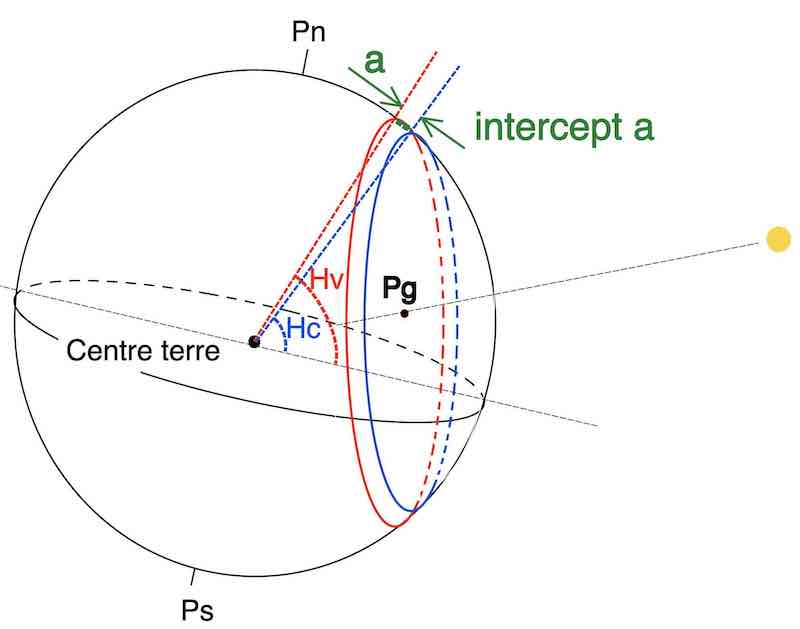



Le principe étape 3 : suite

Imaginez que votre position estimée soit en réalité votre position réelle.
Vous utilisez alors un sextant pour mesurer la hauteur du Soleil (Hv), puis vous calculez la hauteur (Hc) à l’aide des formules.
Dans ce cas, la hauteur vraie correspond exactement à la hauteur calculée.


Maintenant, l’intercept sera nul, et les deux lignes de positions (droites de hauteur) se rejoignent et passent sur la position estimée, perpendiculairement à la direction du soleil


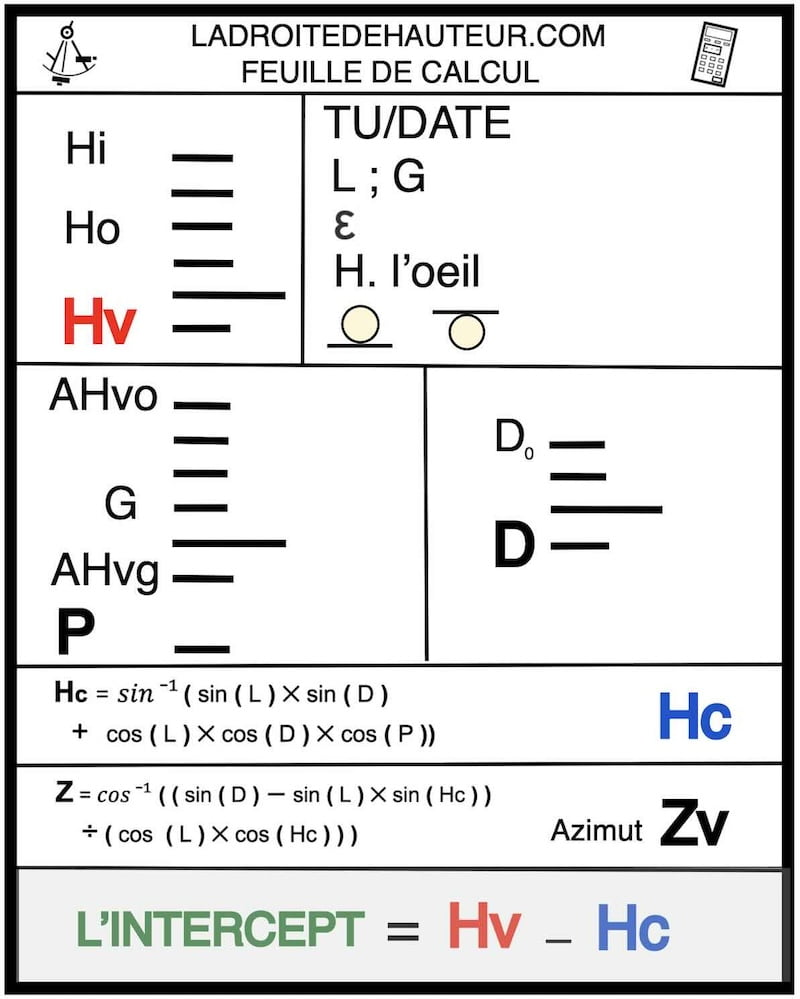
LE PRINCIPE de la droite de hauteur:
Comment calculer l’intercept ?


Pour mieux comprendre le 1′,5 mille nautique
voir la définition « mille marin » sur le lien ici
L’intercept positive et négative:
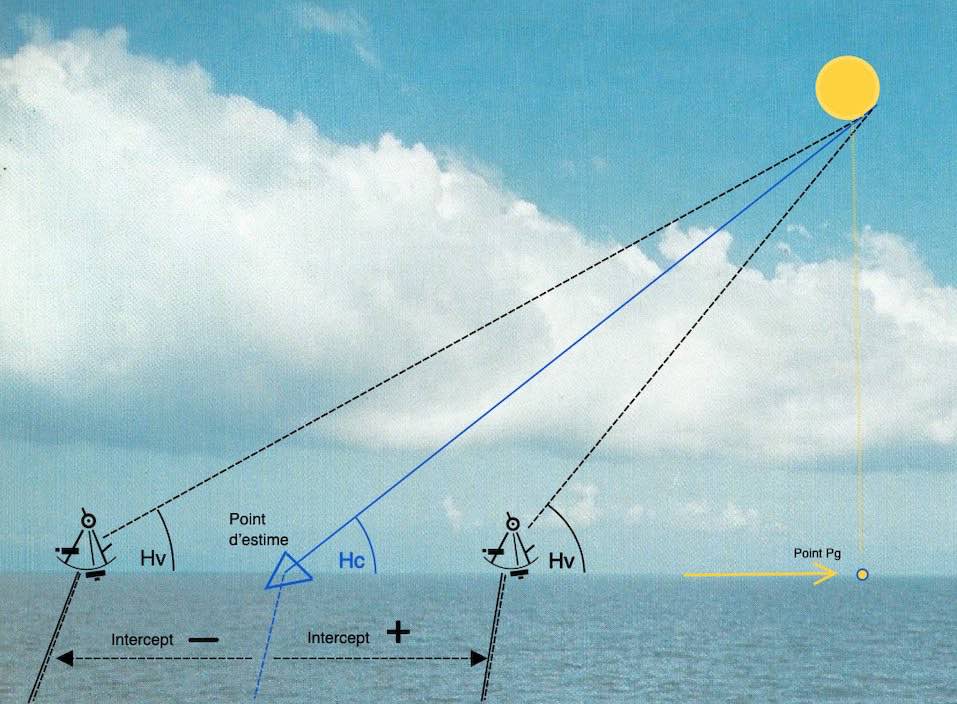
1 L’intercept (+) Hv > Hc


2 L’intercept ( – ) Hc >Hv


Comment tracer la droite de hauteur dans la carte
quatre exemples
+ intercept vers l’astre (positif)
– intercept à l’opposé de l’astre (négatif)
