
Le canevas et la navigation astronomique: Les canevas sont conçus pour la navigation en haute mer.
Les marins utilisent fréquemment ces canevas pour représenter les droites de hauteur obtenues à travers les méthodes de navigation céleste.
Comme on peut le voir sur cette page, ces canevas sont élaborés à proximité de notre latitude estimée.
Dans ce site web, nous utilisons la méthode de Marcq Saint-Hilaire dans notre exercice nommé « La Rochelle » pour calculer ces droites de hauteur et qui est d’ailleurs le but principal de ce site

Puisque les aides à la navigation visuelles, les lignes côtières et les profondeurs d’eau n’ont aucune utilité en navigation hauturière, et que les cartes de navigation océanique ont des échelles inadaptées pour tracer les droites de hauteur, celles-ci sont représentées sur un canevas avant d’être reportées sur la carte.


voir définition mille nautique
Consultez également ma page sur l’utilisation des feuilles de traçage universelles (Universal plotting sheets), qui sont des modèles préexistants visant le même objectif : tracer des droites de hauteur, effectuer leur transport et déterminer votre position en mer
Le canevas et la navigation astronomique:
Construction d’un canevas mercator pour une latitude donnée

Comme illustré dans l’image ci-dessous, les lignes de longitude ont des distances égales entre elles, mais les distances entre chaque ligne de latitude augmentent à mesure que les lignes s’approchent des pôles.
Cependant, seul sur l’équateur les lignes de latitude et de longitude sont à la même distance.
EXEMPLE 1

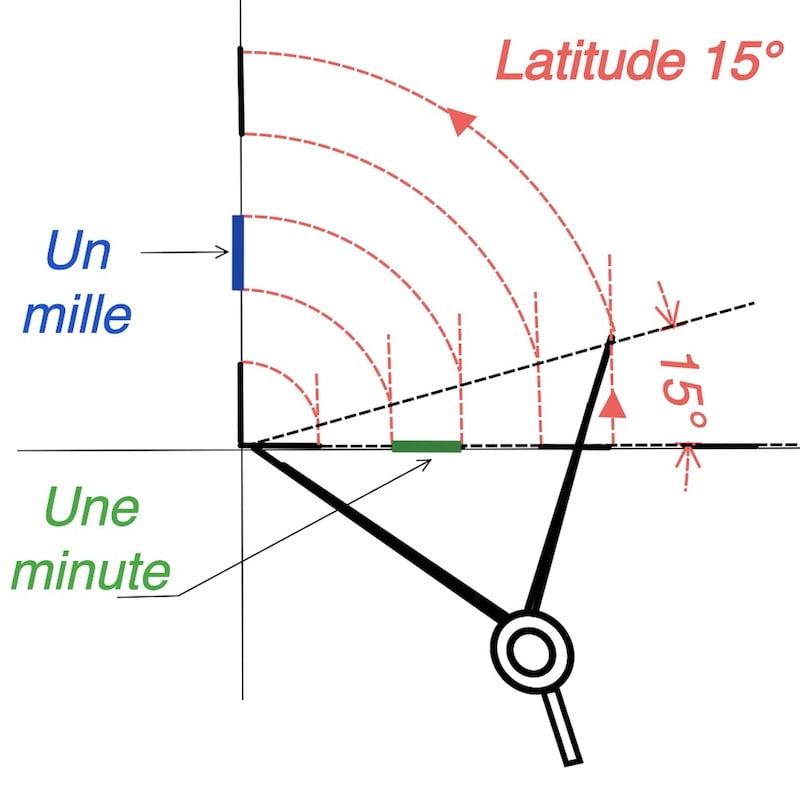
Choisis la longueur d’une minute sur l’échelle de longitude et trace des lignes verticales.
Trace la ligne sous un angle de 15°.
Utilise le compas pour établir l’échelle de latitude.
EXEMPLE 2

La longueur de la minute sur l’échelle de longitude est à votre choix ; par exemple, vous pourriez prendre un centimètre comme longueur d’une minute à la latitude 65°. La longueur d’un mille sur l’échelle de latitude sera, dans ce cas, d’environ 2,4 cm.

Choix de l’échelle de tracé
Ce choix dépend de la longueur de l’intercept et de la distance parcourue entre la première et la deuxième droite de hauteur, ainsi que de la surface de votre feuille de traçage.
Latitude ≈ 27° N

J’ai choisi A = 2cm → B = 2.25 cm
Exemple d’application
Latitude ≈ 27° N

Le mille marin et la latitude
Néanmoins, la longueur d’un mille marin dépend de la latitude et de la valeur attribuée à la minute, et elle augmente davantage aux latitudes élevées.
En conclusion, la longueur d’un mille sur une carte marine varie entre les basses et les hautes latitudes, mais la valeur du mille marin reste constante partout sur Terre à 1852 mètres pour un mille.

Tracé d’une droite de hauteur sur un canevas
EXEMPLE 1
Avec l’aide de notre feuille de calcul, nous avons trouvé l’intercept à +3′ et l’azimut à 029°. (Latitude approximative 65°).
Maintenant, nous dessinons ceci sur notre canevas à soixante-cinq degrés.

canevas 65° / intercept vers le soleil

EXEMPLE 2
Avec l’aide de notre feuille de calcul, nous avons trouvé l’intercept à -6′,7 et l’azimut à 111°. (Latitude approximative 15°).
Maintenant, nous dessinons ceci sur notre canevas à quinze degrés.

canevas 15° / intercept à l’opposé du soleil
Le canevas et la navigation astronomique:

On peut également calculer la longueur d’un mille après avoir choisi la longueur d’une minute sur notre canevas.
Rappelez-vous que cette minute est une valeur fixe choisie par le constructeur.
Donc, sur un canevas, la longueur d’un mille dépend à la fois de la latitude et de l’échelle choisie pour la minute de longitude. Plus la latitude est élevée, plus cette longueur est importante, bien que le mille marin reste défini partout sur Terre à 1 852 m.
formule:
minute / cos (L) → mille
- longueur minute sur l’échelle des longitudes
- longueur mille sur l’échelle des latitudes
- (L) la latitude estimée, arrondie au degré près



La déformation des surfaces sur une carte de Mercator devient plus prononcée à mesure que l’on s’éloigne de l’équateur.
Aux latitudes moyennes, la distorsion est encore relativement limitée, mais elle devient plus significative aux hautes latitudes.
Généralement, au-delà d’environ 70 degrés de latitude nord ou sud, la distorsion devient très importante sur une carte de Mercator et non utilisable. Aux pôles, elle devient infinie.